In triangle ABC, AD and aEarn ABCD is a rhombus, AB is produced In the figure bisector of B and D of quadrilateral ABCD meet CO and AB produced and Q respectively. Prove that angle P t angle Q (angle ABC t le ADC). A
Step by step video solution for In triangle ABC, AD and aEarn ABCD is a rhombus, AB is produced In the figure bisector of B and D of quadrilateral ABCD meet CO and AB produced and Q respectively. Prove that angle P t angle Q (angle ABC t le ADC). A by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
A∠C+∠DB12(∠C+∠D)C12∠C+13∠DD13∠C+12∠D
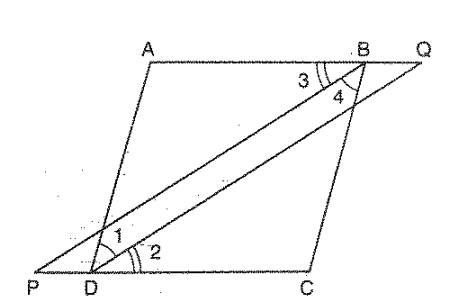
In Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at Pand Q respectively. Prove that : ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionIn the figure, bisectors of ∠Band∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=1/2(∠ABC+∠ADC)
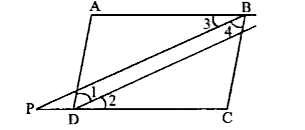
Given: In the given figure, bisectors of ∠Band∠D of a quadrilateral ABCD meet CD and AB produced at P and Q respectively.
To prove: ∠P+∠Q=12(∠ABC+∠ADC)
View SolutionAD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AD is parallel to BC.
View Solution
