If the Boolean expression
(p⊕q)∧(~p□q) is equivalent to p∧q where ⊕,□ε{∧,∨} then the ordered pair (⊕,□) is
A
(∧,∧)
B
(∧,∨)
C
(∨,∧)
D
(∨,∨)
Text Solution
The correct Answer is:b
(p∧q)∧(~p∨q) can be verified using tables to be equivalent to (p∧q) as shown below.
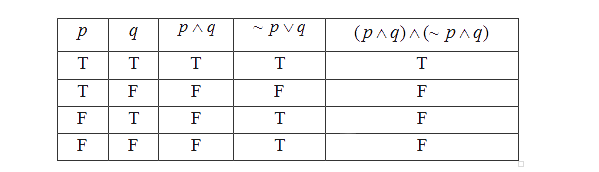
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The Boolean expression ~(p∨q)∨(~p∧q) is equivalent to-
A~pBpCqD~qThe boolean expression ~(p⇒(~q)) is equivalent to
Ap∧qBq⇒~pCp∨qD(~p)⇒qThe Boolean expression ~(p∨q)∨(~p∧q) is equivalent to :
ApBqC~qD~p
The negation of the Boolean expression p∨(~p∧q) is equivalent to :
View Solution~(p∨q)∨(~p∧q) is equivalent to
View SolutionIf the expression (p⊕q)∧(~p0.q) is equivalent of p∧q (where ⊙,⊕,∈{∨,∧},)then the ordered pair (⊕,⊙) is equivalent to
View SolutionThe Boolean Expression (p∧~q)∨q∨(~p∧q)is equivalent to:
View SolutionThe Boolean expression ~(p⇒(~q)) is equivalent to:
View Solution
