The length of the chord of the parabola $x^{2} = 4 y$ having equations $x - \sqrt{2} y + 4 \sqrt{2} = 0$ is

A

$8 \sqrt{2}$

B

$2 \sqrt{11}$

C

$6 \sqrt{3}$

D

$3 \sqrt{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$x^{2} = 4 y ... . . (i)$
$x - \sqrt{2} y + 4 \sqrt{2} = 0$
$x = \sqrt{2} y - 4 \sqrt{2} ... ... . (i i)$
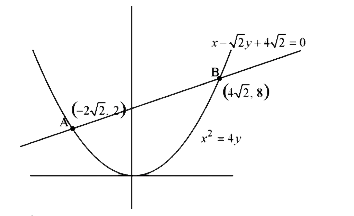
For Point of intersection we will solve both the equation
${(\sqrt{2} y - 4 \sqrt{2})}^{2} = 4 y$
$2 y^{2} + 32 - 16 y = 4 y$
$y^{2} - 10 y + 16 = 0$
$y^{2} - 2 y - 8 y + 16 = 0$
$(y - 2) (y - 8) = 0$
$y = 2, y = 8$
$x^{2} = 8$
$x = \pm 2 \sqrt{2}$
$A = - 2 \sqrt{2}, 2)$
$x^{2} = 32$
$x = \pm 4 \sqrt{2}$
$B (4 \sqrt{2}, 8)$
${(dist)}_{A B} = \sqrt{{(4 \sqrt{2} - (- 2 \sqrt{2}))}^{2} + {(8 - 2)}^{2}}$
$= \sqrt{36 \times 2 + 36}$
dist $= 6 \sqrt{3}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The length of the latus - rectum of the parabola $4 y^{2} + 2 x - 20 y + 17 = 0$ is
A2
B $\frac{1}{8}$
C $\frac{1}{2}$
D4
Question 2 - Select One
The length of latus-rectum of the hyperbola $x^{2} - 2 y^{2} - 2 x + 8 y - 1 = 0$ is
(i) $\sqrt{6}$
(ii) $4 \sqrt{3}$
(iii) 4
(iv) 3
A $\sqrt{6}$
B $4 \sqrt{3}$
C4
D3

VMC MODULES ENGLISH-JEE MAIN REVISION TEST-3 (2020)-MATHEMATICS (SECTION 2)

Home
Ask Doubt
Profile