If the area enclosed between the curves y=kx2 and x=ky2, where k>0, is 1 square unit. Then k is: (a) 1√3 (b) √32 (c) 2√3 (d) √3
√32
2√3
√3
1√3
The correct Answer is:D
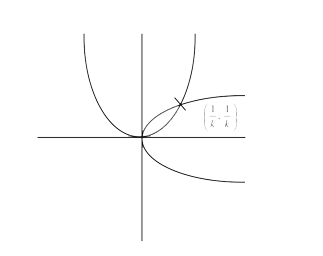
Since y=kx2 and x=ky2 intersect at (1k,1k)
∫1k0(√xk−kx2)dx=1
x22k−kx33=1
23k2−13k2=1
13k2=1
k2=13
k=1√3
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 29 (2020)EXERCISE - MATHEMATICS25videos
JEE MAIN REVISION TEST - 29 (2020)
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Mathematics (Section - 2) Numercial type questions5videos
JEE MAIN REVISION TEST - 7|JEE - 2020
Similar Questions
The rationalisation factor of √3 is
(a)−√3
(b) 1√3
(c) 2√3
(d) −2√3View SolutionTangent of acute angle between the curves y=∣∣x2−1∣∣ and y=√7−x2 at their points of intersection is (a) 5√32 (b) 3√52 5√34 (d) 3√54
View SolutionTangent of acute angle between the curves y=∣∣x2−1∣∣ and y=√7−x2 at their points of intersection is 5√32 (b) 3√52 5√34 (d) 3√54
View SolutionThe rationalisation factor of 2+√3 is
(a)2−√3
(b) √2+3
(c) √2−3
(d) √3−2View SolutionThe area enclosed by the curves y=sinx+cosxandy=|cosx−sinx| over the interval [0,π2] is (a) 4(√2−1) (b) 2√2(√2−1) (c) 2(√2+1) (d) 2√2(√2+1)
View SolutionThe value of √3−2 √2 is
(a)√2−1
(b) √2+1
(c) √3−√2
(d) √3+ √2View SolutionShow that the area enclosed between the curve y2=12(x+3)andy2=20(5−x) is 64√53
View SolutionThe length of the chord of the parabola y2=x which is bisected at the point (2, 1) is (a)2√3 (b) 4√3 (c) 3√2 (d) 2√5
View SolutionThe value of sin(14sin−1(√638)) is (a) 1√2 (b) 1√3 (c) 12√2 (d) 13√3
View SolutionThe area bounded by the curve x2=ky,k>0 and the line y=3 is 12unit2. Then k is (A) 3 (B) 3√3 (C) 34 (D) none of these
View Solution

