1g of same non volatile solute is added to 100g of two different solvents A and B. Kb of A:B=1:5
Find out (ΔTb)A(ΔTb)B
1:0.2
1:5
5:1
10:1
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the given data
We have:
- Mass of non-volatile solute (W) = 1 g
- Mass of solvent A = 100 g
- Mass of solvent B = 100 g
- Kb of solvent A to solvent B = 1:5
Step 2: Write the formula for boiling point elevation
The change in boiling point (ΔTb) is given by the formula:
ΔTb=Kb×m
where m is the molality of the solution.
Step 3: Calculate molality
Molality (m) is defined as:
m=Number of moles of soluteMass of solvent in kg
The number of moles of solute can be calculated as:
Number of moles=WM
where M is the molecular weight of the solute.
Since the mass of the solvent is the same for both A and B (100 g = 0.1 kg), we can express molality as:
m=1 gM g/mol÷0.1 kg=10M
Step 4: Calculate ΔTb for both solvents
For solvent A:
ΔTbA=KbA×m=KbA×10M
For solvent B:
ΔTbB=KbB×m=KbB×10M
Step 5: Find the ratio ΔTbAΔTbB
Now, we can find the ratio of the boiling point elevations:
ΔTbAΔTbB=KbA×10MKbB×10M=KbAKbB
Step 6: Substitute the given ratio of Kb
Given that KbAKbB=15:
ΔTbAΔTbB=15
Final Answer
Thus, the final result is:
ΔTbAΔTbB=15
---
We have:
- Mass of non-volatile solute (W) = 1 g
- Mass of solvent A = 100 g
- Mass of solvent B = 100 g
- Kb of solvent A to solvent B = 1:5
The change in boiling point (ΔTb) is given by the formula:
ΔTb=Kb×m
where m is the molality of the solution.
Molality (m) is defined as:
m=Number of moles of soluteMass of solvent in kg
The number of moles of solute can be calculated as:
Number of moles=WM
where M is the molecular weight of the solute.
m=1 gM g/mol÷0.1 kg=10M
For solvent A:
ΔTbA=KbA×m=KbA×10M
ΔTbB=KbB×m=KbB×10M
Now, we can find the ratio of the boiling point elevations:
ΔTbAΔTbB=KbA×10MKbB×10M=KbAKbB
Given that KbAKbB=15:
ΔTbAΔTbB=15
Thus, the final result is:
ΔTbAΔTbB=15
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 13Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 13Exercise:CHEMISTRY (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 12 Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 12 Exercise:CHEMISTRY
Explore 25 Videos
- JEE MAIN REVISION TEST - 18Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 18Exercise:CHEMISTRY - SECTION 2
Explore 5 Videos
Similar Questions
1g of a non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, ΔTb(A)ΔTb(B) is
View SolutionTwo solutions of non-volatile and non-electrolyte solute A and B are prepared separately. The molar mass ratio MAMB=13. Both are prepared as 5% by weight solution in water. Then what is the ratio of freezing point depresions, (ΔTf)A(ΔTf)B of the solutions?
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
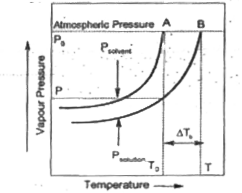
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal to
View SolutionThe boiling a point of benzene is 353.23K. When 1.80 g of a non-volatile solute was dissolved in 90 g of benzene, the boiling point is raised to 354.11 K. Calculate the molar mass of the solute. Kb for benzene is 2.53 K kg mol−1.
View SolutionA system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vapourizes to form a more disordered gas. When a solute is present, there is additional contribution to the entropy of the liquid due to increased randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas. Thus, a solute (non-volatile) lowers the vapour pressure of a liquid, and hence a higher boiling point of the solution.
Similarly, the greater randomness of the solution opposes the tendercy to freeze. In consequence, a lower temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution. The elevation in boiling point (ΔTb) and depression in freezing point (ΔTf) of a solution are the colligative properties which depend only on the concentration of particles of the solute and not their identity. For dilute solutions, (ΔTb) and (ΔTf) are proportional to the molarity of the solute in the solution.
Dissolution of a non-volatile solute into a liquid leads to
View SolutionA system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vapourizes to form a more disordered gas. When a solute is present, there is additional contribution to the entropy of the liquid due to increased randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas. Thus, a solute (non-volatile) lowers the vapour pressure of a liquid, and hence a higher boiling point of the solution.
Similarly, the greater randomness of the solution opposes the tendercy to freeze. In consequence, a lower temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution. The elevation in boiling point (ΔTb) and depression in freezing point (ΔTf) of a solution are the colligative properties which depend only on the concentration of particles of the solute and not their identity. For dilute solutions, (ΔTb) and (ΔTf) are proportional to the molarity of the solute in the solution.
A mixture of two immiscible liquids at a constant pressure of 1.0atm boils at temperature
View SolutionA system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vapourizes to form a more disordered gas. When a solute is present, there is additional contribution to the entropy of the liquid due to increased randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas. Thus, a solute (non-volatile) lowers the vapour pressure of a liquid, and hence a higher boiling point of the solution.
Similarly, the greater randomness of the solution opposes the tendercy to freeze. In consequence, a lower temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution. The elevation in boiling point (ΔTb) and depression in freezing point (ΔTf) of a solution are the colligative properties which depend only on the concentration of particles of the solute and not their identity. For dilute solutions, (ΔTb) and (ΔTf) are proportional to the molarity of the solute in the solution.
To aqueous solution of Nal, increasing amounts of solid Hgl2 is added. The vapour pressure of the solution
View SolutionAn aqueous solution of a non-volatile solute boils at 100.17∘C. At what temperature will the solution freeze? (Given: Kb=0.512 and Kf=1.86)
View SolutionFigure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
View SolutionIf A and B are any two matrices of the same order, then (AB)=A'B'
View Solution
