Two sources of sound are moving in opposite directions with velocities V1 and V2(V1>V2). Both are moving away from a stationary observer. The frequency of both the source is 1700Hz. What is the value of (V1−V2) so that the beat frequency observed by the observer is 10Hz. Vsound=340m/s and assume that V1 and V2 both are very much less than Vsound.
1m/s
2m/s
3m/s
4m/s
The correct Answer is:B
To solve the problem, we need to determine the difference in velocities V1−V2 such that the beat frequency observed by a stationary observer is 10 Hz. We will use the given information and the formula for the frequency heard by the observer.
1. Identify the Given Values:
- Frequency of both sources, f=1700 Hz
- Velocity of sound, vsound=340 m/s
- Beat frequency, fb=10 Hz
- Velocities of the sources, V1 and V2 (with V1>V2)
2. Formula for Frequency Heard by the Observer:
The frequency heard by the observer from each source can be calculated using the Doppler effect formula:
f′=f⋅vsound+vobservervsound−vsource
Since the observer is stationary, vobserver=0:
- For source 1 (moving away):
f1=f⋅vsoundvsound+V1=1700⋅340340+V1
- For source 2 (moving away):
f2=f⋅vsoundvsound+V2=1700⋅340340+V2
3. Calculate the Beat Frequency:
The beat frequency fb is given by the difference in frequencies heard from the two sources:
fb=|f2−f1|=10 Hz
Substituting for f1 and f2:
10=1700(340340+V2−340340+V1)
4. Simplifying the Expression:
Factor out 1700:
10=1700(340(340+V1)−340(340+V2)(340+V1)(340+V2))
This simplifies to:
10=1700⋅340(V2−V1)(340+V1)(340+V2)
5. Assuming V1 and V2 are Much Less than vsound:
Since V1 and V2 are much less than 340 m/s, we can use the approximation:
(340+V1)≈340and(340+V2)≈340
Thus, the equation simplifies to:
10=1700⋅340(V2−V1)3402
Rearranging gives:
10=1700⋅V2−V1340
6. Solving for V1−V2:
Rearranging gives:
V1−V2=10⋅3401700
Simplifying:
V1−V2=2 m/s
Final Answer:
The value of V1−V2 is 2 m/s.
- Frequency of both sources, f=1700 Hz
- Velocity of sound, vsound=340 m/s
- Beat frequency, fb=10 Hz
- Velocities of the sources, V1 and V2 (with V1>V2)
The frequency heard by the observer from each source can be calculated using the Doppler effect formula:
f′=f⋅vsound+vobservervsound−vsource
Since the observer is stationary, vobserver=0:
- For source 1 (moving away):
f1=f⋅vsoundvsound+V1=1700⋅340340+V1
- For source 2 (moving away):
f2=f⋅vsoundvsound+V2=1700⋅340340+V2
The beat frequency fb is given by the difference in frequencies heard from the two sources:
fb=|f2−f1|=10 Hz
Substituting for f1 and f2:
10=1700(340340+V2−340340+V1)
Factor out 1700:
10=1700(340(340+V1)−340(340+V2)(340+V1)(340+V2))
This simplifies to:
10=1700⋅340(V2−V1)(340+V1)(340+V2)
Since V1 and V2 are much less than 340 m/s, we can use the approximation:
(340+V1)≈340and(340+V2)≈340
Thus, the equation simplifies to:
10=1700⋅340(V2−V1)3402
Rearranging gives:
10=1700⋅V2−V1340
Rearranging gives:
V1−V2=10⋅3401700
Simplifying:
V1−V2=2 m/s
The value of V1−V2 is 2 m/s.
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 1 | JEE - 2020 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 1 | JEE - 2020 EXERCISE - PHYSICS ( SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 1 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 1 (2020)EXERCISE - PHYSICS - SECTION 2
5 Videos
- JEE MAIN REVISION TEST - 10| JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 10| JEE -2020EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
Two sound sources are moving in opposite directions with velocities v1andv2(v1>v2) . Both are moving away from a stationary observer. The frequency of both the sources is 900 Hz. What is the value of v1−v2 so that the beat frequency aboserved by the observer is 6 Hz. speed of sound v= 300 m/s given ,that v1andv2<<v
View SolutionTwo sound sources are moving away from a stationary observer in opposite direction with velocities V1 and V2(V1>V2). The frequency of both the sources is 900 Hz. V1 and V2 are both quite less than speed of sound, V=300ms. Find the value of (V1−V2) so that beat frequency observed by observer is 9 Hz. (in m/s).
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View SolutionGiven frequency of source f=100Hz,vs=20m/sand v=330m/s.Thebeatequenciesf_(1)andf_(2) are
View SolutionA source of sound of frequency 300 Hz and a receiver are located along the same line normal to the wall as shown in the figure. Both the source and the receiver are stationary and the wall receeds from the source with velocity 20ms−1.If the beat frequency registered by the receiver is 240x Hz then x is :
(Assume Vsound=300 m/s).

View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionA stationary particle explodes into two particle of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
View SolutionTwo masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
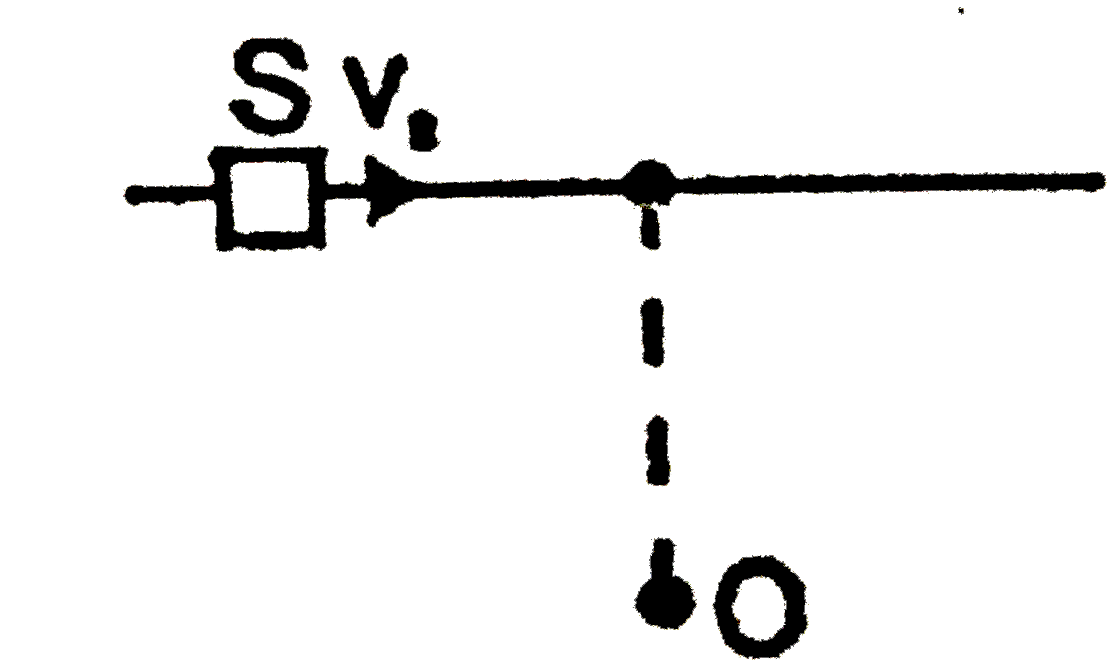
View Solution
