If →a=ˆi+ˆj+ˆk&→b=ˆi−ˆj+ˆk are the sides of AB & AC of ΔABC , if AD is the angle bisector of ∠BAC where D lies on BC, then length of AD is
A
1
B
√2
C
√3
D
2
Video Solution
Text Solution
The correct Answer is:B
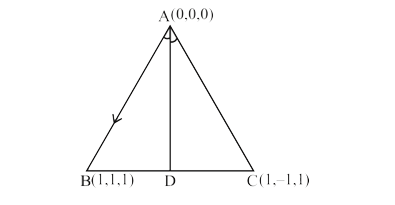
Let A is at origin then B(1,1,1) and C(1,-1,1) also AB=√3 AC=√3
Hence bisector theorem
BDDC=ABAC=1
∴D(1,0,1) ∴AD=√1+0+1=√2.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
If →a=ˆi+ˆj+ˆk & →B=ˆi−ˆj+ˆk are the sides of AB & AC of △ABC if AD is the angle bisector of ∠BAC where D lies on BC, then length of AD is
View SolutionIf →a=2ˆi−3ˆj−1ˆkand→b=ˆi+4ˆj−2ˆk then →a×→b is
View SolutionIf →a=2ˆi−3ˆj−ˆk and →b=ˆi+4ˆj−2ˆk, then →a×→b is
View SolutionIf →a=2ˆi−ˆj+2ˆkand→b=−ˆi+ˆj−ˆk calculate →a+→b
View SolutionIf →a=3ˆi+ˆj−4ˆkand→b=6ˆi+5ˆj−2ˆk find ∣∣→aX→b∣∣
View Solutionfind →A×→B if →A=ˆi−2ˆj+4ˆkand→B=3ˆi−ˆj+2ˆk
View SolutionIf →A=3ˆi+ˆj+2ˆk and →B=2ˆi−2ˆj+4ˆk, then value of ∣∣→AX→B∣∣ will be
View SolutionLet →a=ˆi+3ˆj+7ˆkand→b=7ˆi−ˆj+8ˆk find the projection of →a on →b
View SolutionLet →a=ˆi+3ˆj+7ˆkand→b=7ˆi−ˆj+8ˆk find the projection of →b on →a
View SolutionIf →A=(2ˆi+3ˆj+5ˆk) and →B=(ˆi+6ˆj+6ˆk), then projection of →A on →B would be
View Solution

