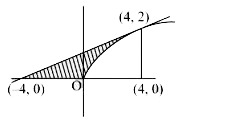
The area (in square units) of the region bounded by $y = \sqrt{x}, x \geq 0$ tangent to it at $(4, 2)$ & x-axis is :

A

$\frac{16}{3}$

B

$\frac{2}{3}$

C

$\frac{8}{3}$

D

$\frac{32}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$\frac{d y}{d x} = \frac{1}{2 \sqrt{x}} = \frac{1}{4} a t (\frac{4}{2})$
Equation of tangent is $x - 4 y + 4 = 0$
shaded area = $\frac{1}{2} \times 8 \times 2 - \int_{0}^{4} \sqrt{x} d x = 8 - {∣ ∣ ∣ \frac{2}{3} x^{3 / 2} ∣ ∣ ∣}_{0}^{3 / 2} = 8 - \frac{2}{3} c o d t 4.2 = \frac{8}{3}$ square units.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-JEE MAIN REVISION TEST - 18-MATHEMATICS - SECTION 2

Home
Ask Doubt
Profile