Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is
180
210
170
190
The correct Answer is:C
To solve the problem, we need to determine the total number of beams that can be connected between the pillars, excluding the beams that connect adjacent pillars. Here’s the step-by-step solution:
Step 1: Calculate the total number of ways to connect the pillars
We have 20 pillars, and we want to connect each pillar to every other pillar. The number of ways to choose 2 pillars from 20 to connect them with a beam is given by the combination formula:
Total connections=(202)
Calculating this:
(202)=20×192×1=190
Step 2: Identify the number of adjacent pillars
In a circular arrangement, each pillar has exactly 2 adjacent pillars (one on each side). Since there are 20 pillars, the total number of adjacent connections (beams) is:
Adjacent beams=20
Step 3: Calculate the number of non-adjacent beams
To find the number of beams that connect non-adjacent pillars, we subtract the number of adjacent beams from the total connections:
Non-adjacent beams=Total connections−Adjacent beams
Substituting the values we calculated:
Non-adjacent beams=190−20=170
Conclusion
The total number of beams connecting non-adjacent pillars is 170.
---
We have 20 pillars, and we want to connect each pillar to every other pillar. The number of ways to choose 2 pillars from 20 to connect them with a beam is given by the combination formula:
In a circular arrangement, each pillar has exactly 2 adjacent pillars (one on each side). Since there are 20 pillars, the total number of adjacent connections (beams) is:
To find the number of beams that connect non-adjacent pillars, we subtract the number of adjacent beams from the total connections:
The total number of beams connecting non-adjacent pillars is 170.
Topper's Solved these Questions
- PERMUTATION & COMBINATIONBOOK - VMC MODULES ENGLISHCHAPTER - PERMUTATION & COMBINATIONEXERCISE - LEVEL-2
88 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- PROBABILITYBOOK - VMC MODULES ENGLISHCHAPTER - PROBABILITYEXERCISE - JEE ADVANCED (ARCHIVE)
102 Videos
Similar Questions
The angle of elevation of the top of an incomplete vertical pillar at a horizontal distance of 50 m from its base is 45∘. If the angle of elevation of the top of the complete pillar the same point is to be 60∘,then the height of the incomplete pillar is to be increased by
View SolutionThe angle of elevation of the top of an incomplete vertical pillar at a horizontal distance of 100 m from its base is 45∘. If the angle of elevation of the top of the complete pillar at the same point is to be 60∘, then the height of the incomplete pillar is to be increased by
View Solution
Knowledge Check
Most chickens reach maturity and begin laying eggs at around 20 weeks of age. From this point forward, however, as the chicken ages,its eges its egg production decreases. A farmer was given a flock of 100 chickens (all of which were the same age) and asked to meaure daily egg output for the entire flock at random intervals starting at maturity until the chickens were 70 weeks old. The data are recorded in the scatteplot below and the line of best fit has been drawn.
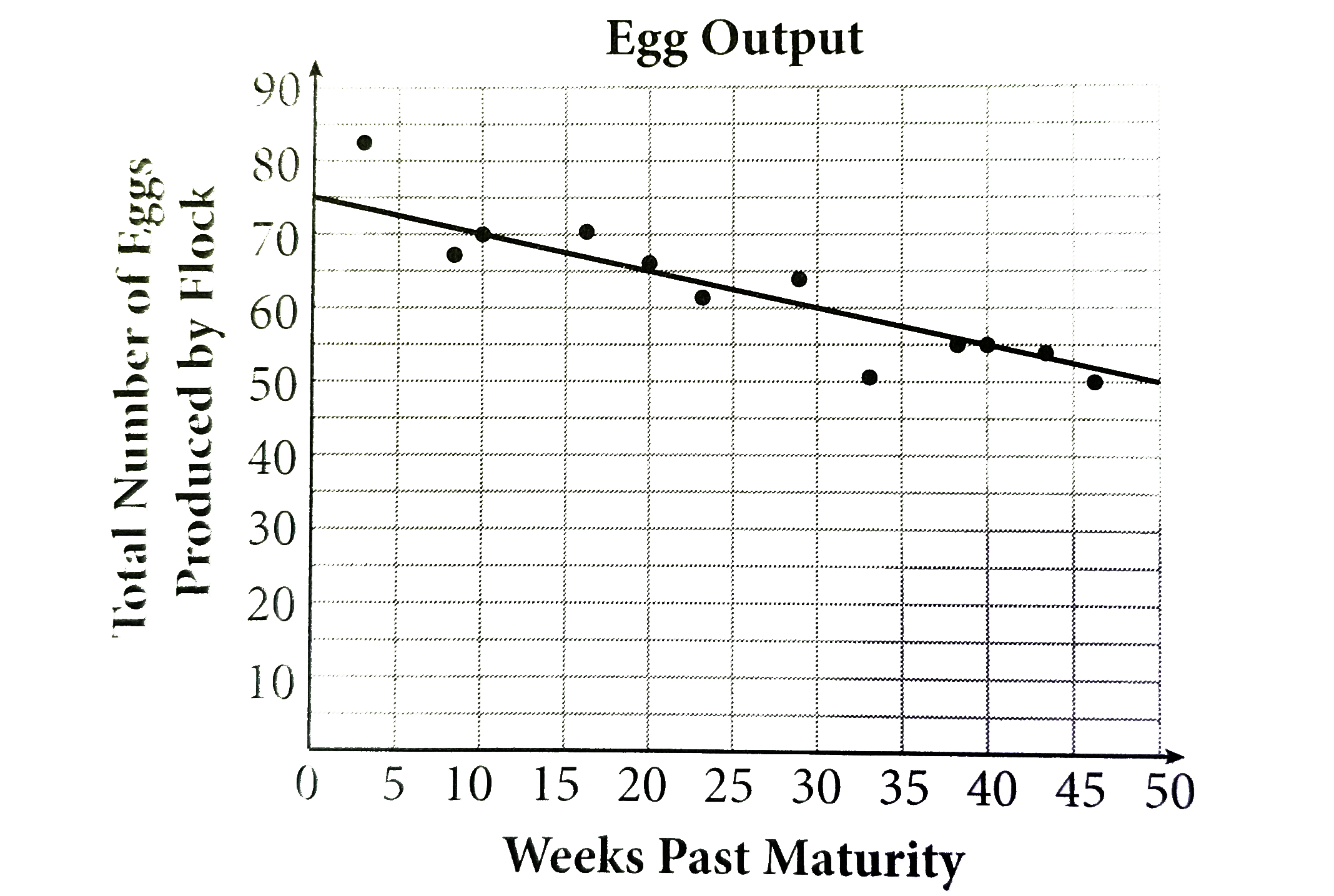
Based on the line of bast fit, what is the predicted number of eggs that will be produced by the flock when it is 33 weeks past maturity ?A33B50C58D64For Question 19-20 use the figure above

A lamp shade with a circular base is an example of a solid shape called a frustrum. In the figure above, the shaded region represents a frustrum of a right cone in which the portion of the original cone that lies 12 inches below its vertex has been cut off by slicing plane (not shown) parallel to the base.
Q. If the height and slant height of the frustrum are 8 inches and 10 inches, respectively, what is the number of inches in the radius length, R, of the original cone?A9B12C15D8
The pillars of a temple are cylindrically shaped. If each pillar has a circular base of radius 20cm and height 10m. How much concrete mixture would be required to build 14 such pillars?
View SolutionA small ball is projected at an angle α with an initial velocity u between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic and distance between the walls be d2, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

View SolutionMost chickens reach maturity and begin laying eggs at around 20 weeks of age. From this point forward, however, as the chicken ages,its eges its egg production decreases. A farmer was given a flock of 100 chickens (all of which were the same age) and asked to meaure daily egg output for the entire flock at random intervals starting at maturity until the chickens were 70 weeks old. The data are recorded in the scatteplot below and the line of best fit has been drawn.

How many times did the farmer's data differ by more than 5 eggs from the number of eggs predicted by the line of best fit ?
View SolutionThe pillars of a temple are cylindrically shaped (see Fig. 13.26). If each pillar has a circular base of radius 20 cm and height 10 m, how much concrete mixture would be required to build 14 such pillars?
View SolutionOne end of a 60m long rope of mass 1.8 kg is tied to a rigid horizontal support held high above the ground. The rope hangs vertically and kept taut by a weight 'W' suspended at its lower end. A person jerks the lower end of the rope sideways in a sinusoidal manner and a transverse wave of frequency 2 Hz and amplitude 10cm passes along the rope such that there are 2 cycles of the wave in the total length of the rope. Neglecting the weight of the rope as compared to the suspended weight W and with g = 10m/s2, answer the following questions. (S=75×10−4m2)

In the questions above, weight of the rope has been neglected as compared to the suspended weight. However, if we also account for the weight of the rope. the speed of the wave at the top of the rope will be
View SolutionThis interference film is used to measure the thickness of slides, paper, etc. The arrangement is as shown in fig. For the sake of clarity, the two strips are shown thick. Consider the wedge formed in between strips 1 and 2. If the interference pattern because of the two waves reflected from wedge surface is observed, then from the observed data we can compute thickness of paper, refractive index of the medium filled in wedge, number of bonds formed, etc.
Considre the strips to be thick as compared to wavelength of ligth and light is incident normally.
Neglect the effect due to reflection from top surface of strip 1 and bottom surface of strip 2. Take L=5cm and λair=400nm ,h=20mm.
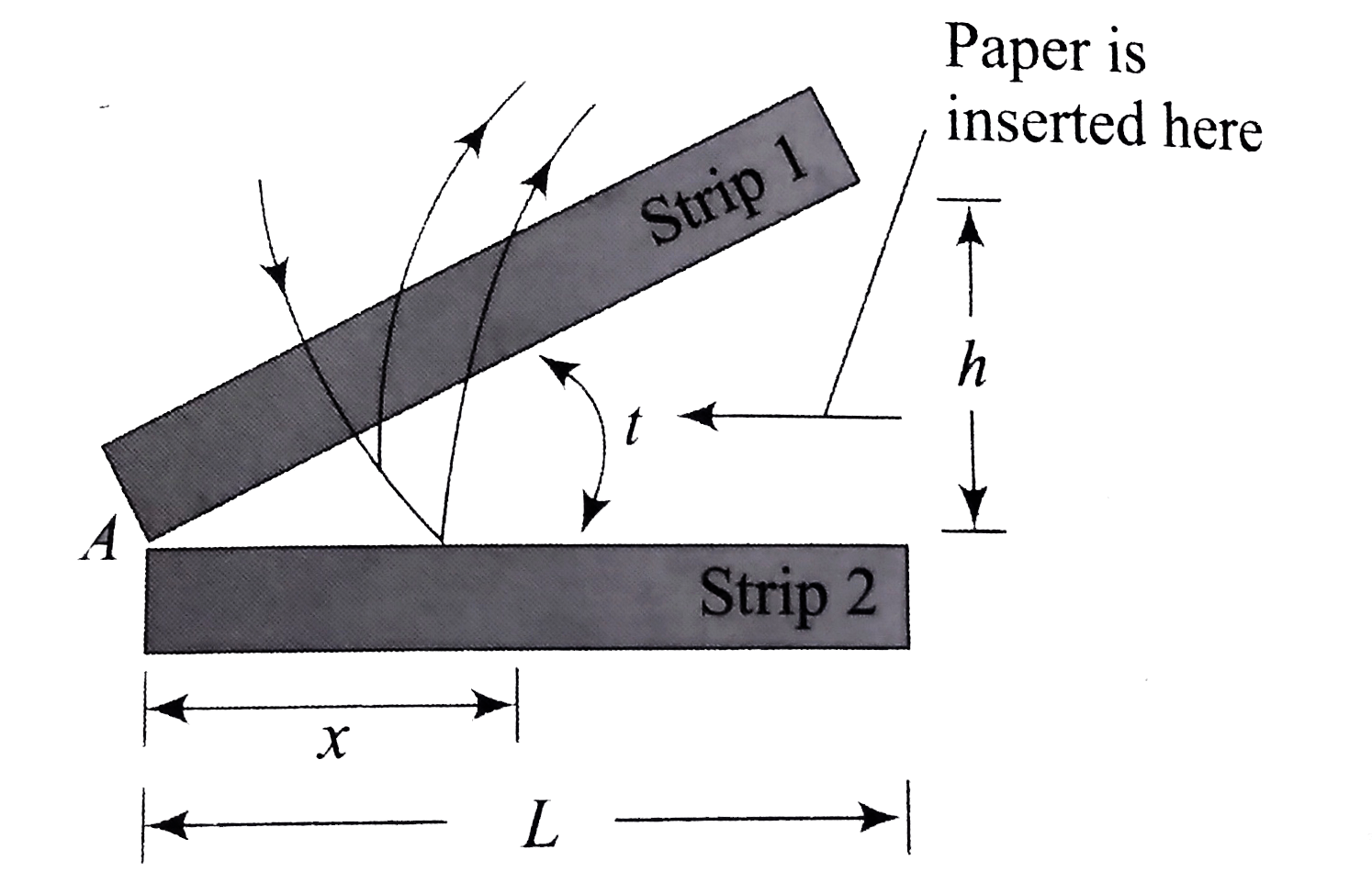
In question 53, if air wedge has been filled with a medium having refractive index 1.3 then find the number of bright bands.
View Solution
