If the lengths of the sides of a triangle are in AP and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is
1:2:√2
1:√3:2
4:5:6
None of these
The correct Answer is:C
To solve the problem, we need to find the ratio of the lengths of the sides of a triangle where the sides are in arithmetic progression (AP) and the greatest angle is double the smallest angle.
1. Define the sides of the triangle:
Let the sides of the triangle be A, B, and C such that A<B<C. Since they are in AP, we can express them as:
A=B−λ,B=B,C=B+λ
where λ is a positive number.
2. Use the angle relationship:
We know that the greatest angle C is double the smallest angle A:
C=2A
3. Apply the Law of Sines:
Using the Law of Sines, we have:
CsinC=AsinA
From the angle relationship, we can also express sinC using the double angle formula:
sinC=sin(2A)=2sinAcosA
4. Set up the equation:
Substituting sinC into the Law of Sines gives:
C2sinAcosA=AsinA
Simplifying this, we get:
C2cosA=A1
Therefore:
C=2AcosA
5. Substituting the expressions for A and C:
Substitute A=B−λ and C=B+λ into the equation:
B+λ=2(B−λ)cos(B−λ)
6. Using the Law of Cosines:
The cosine of angle A can be expressed using the Law of Cosines:
cosA=B2+C2−A22BC
Substitute A=B−λ, B=B, and C=B+λ into this equation.
7. Solve for λ:
After substituting and simplifying, we find that λ=B5.
8. Find the lengths of the sides:
Now substitute λ back into the expressions for A and C:
A=B−B5=4B5,C=B+B5=6B5
9. Determine the ratio of the sides:
The ratio of the sides A:B:C becomes:
4B/5B:BB:6B/5B=4:5:6
Final Answer:
The ratio of the lengths of the sides of the triangle is 4:5:6.
---
Let the sides of the triangle be A, B, and C such that A<B<C. Since they are in AP, we can express them as:
A=B−λ,B=B,C=B+λ
where λ is a positive number.
We know that the greatest angle C is double the smallest angle A:
C=2A
Using the Law of Sines, we have:
CsinC=AsinA
From the angle relationship, we can also express sinC using the double angle formula:
sinC=sin(2A)=2sinAcosA
Substituting sinC into the Law of Sines gives:
C2sinAcosA=AsinA
Simplifying this, we get:
C2cosA=A1
Therefore:
C=2AcosA
Substitute A=B−λ and C=B+λ into the equation:
B+λ=2(B−λ)cos(B−λ)
The cosine of angle A can be expressed using the Law of Cosines:
cosA=B2+C2−A22BC
Substitute A=B−λ, B=B, and C=B+λ into this equation.
After substituting and simplifying, we find that λ=B5.
Now substitute λ back into the expressions for A and C:
A=B−B5=4B5,C=B+B5=6B5
The ratio of the sides A:B:C becomes:
4B/5B:BB:6B/5B=4:5:6
The ratio of the lengths of the sides of the triangle is 4:5:6.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLEBook:VMC MODULES ENGLISHChapter:PROPERTIES OF TRIANGLEExercise:Level - 2
Explore 55 Videos
- PROPERTIES OF TRIANGLEBook:VMC MODULES ENGLISHChapter:PROPERTIES OF TRIANGLEExercise:JEE Main (Archive)
Explore 35 Videos
- PROBABILITYBook:VMC MODULES ENGLISHChapter:PROBABILITYExercise:JEE ADVANCED (ARCHIVE)
Explore 102 Videos
- QUADRATIC EQUATIONS & INEQUATIONS Book:VMC MODULES ENGLISHChapter:QUADRATIC EQUATIONS & INEQUATIONS Exercise:JEE Advance ( Archive )
Explore 20 Videos
Similar Questions
Knowledge Check
The sides of a triangle are in a ratio of 4:5:6. the smallest angle is
A82∘B69∘C56∘D41∘
If the lengths of the sides of a triangle are 3,5,7, then its largest angle of the triangle is
View SolutionIf the sides of a triangle are in A.P. and the greatest angle of the triangle exceeds the least by 90∘, then sine of the third angle is
View SolutionThe lengths of the sides of a triangle are in the ratio 2:3:4. If the perimeter of the triangle is 63 cm, find the lengths of the sides of the triangle.
View SolutionFind the length of the third side of the triangle.
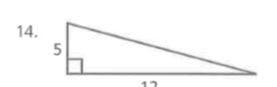
View SolutionFind the length of the third side of the triangle.
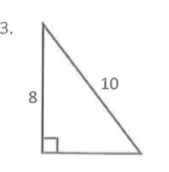
View SolutionThe sides of a triangle are three consecutive numbers and its largest angle is twice the smallest one. Find the sides of the triangle.
View SolutionIf the altitudes of a triangle are in A.P,then the sides of the triangle are in
View Solution