Which of the following holds goods for any triangle ABC ?
cosAa+cosBb+cosCc=a2+b2+c22abc
sinAa+sinBb+sinCc=32R
cosAa+cosBb+cosCc=2abca2+b2+c2
sin2Aa2=sin2Bb2=sin2Cc2
The correct Answer is:A, B
To determine which of the given options holds true for any triangle ABC, we will analyze the sine rule and the cosine rule.
1. Understanding the Sine Rule:
The sine rule states that for any triangle ABC, the ratios of the lengths of the sides to the sines of their opposite angles are equal:
asinA=bsinB=csinC=2R
where R is the circumradius of the triangle.
2. Expressing the Sine Rule:
From the sine rule, we can express:
sinAa=12R,sinBb=12R,sinCc=12R
Thus, we can conclude:
sinAa+sinBb+sinCc=12R+12R+12R=32R
3. Understanding the Cosine Rule:
The cosine rule states that for any triangle ABC:
a2=b2+c2−2bccosA
b2=a2+c2−2accosB
c2=a2+b2−2abcosC
4. Expressing the Cosine Rule:
We can rearrange the cosine rule to express cosA, cosB, and cosC:
cosA=b2+c2−a22bc,cosB=a2+c2−b22ac,cosC=a2+b2−c22ab
5. Analyzing the Options:
- For the sine rule, we derived that sinAa+sinBb+sinCc=32R holds true for any triangle.
- For the cosine rule, the expressions for cosA, cosB, and cosC do not yield a simple sum or ratio that holds universally for all triangles.
6. Conclusion:
The sine rule holds true for any triangle ABC, while the cosine rule does not yield a similar universal statement. Therefore, the correct options are those related to the sine rule.
Final Answer:
The options that hold true for any triangle ABC are based on the sine rule.
The sine rule states that for any triangle ABC, the ratios of the lengths of the sides to the sines of their opposite angles are equal:
asinA=bsinB=csinC=2R
where R is the circumradius of the triangle.
From the sine rule, we can express:
sinAa=12R,sinBb=12R,sinCc=12R
Thus, we can conclude:
sinAa+sinBb+sinCc=12R+12R+12R=32R
The cosine rule states that for any triangle ABC:
a2=b2+c2−2bccosA
b2=a2+c2−2accosB
c2=a2+b2−2abcosC
We can rearrange the cosine rule to express cosA, cosB, and cosC:
cosA=b2+c2−a22bc,cosB=a2+c2−b22ac,cosC=a2+b2−c22ab
- For the sine rule, we derived that sinAa+sinBb+sinCc=32R holds true for any triangle.
- For the cosine rule, the expressions for cosA, cosB, and cosC do not yield a simple sum or ratio that holds universally for all triangles.
The sine rule holds true for any triangle ABC, while the cosine rule does not yield a similar universal statement. Therefore, the correct options are those related to the sine rule.
The options that hold true for any triangle ABC are based on the sine rule.
Topper's Solved these Questions
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - Level - 2
55 Videos
- PROPERTIES OF TRIANGLEBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF TRIANGLEEXERCISE - JEE Main (Archive)
35 Videos
- PROBABILITYBOOK - VMC MODULES ENGLISHCHAPTER - PROBABILITYEXERCISE - JEE ADVANCED (ARCHIVE)
102 Videos
- QUADRATIC EQUATIONS & INEQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - QUADRATIC EQUATIONS & INEQUATIONS EXERCISE - JEE Advance ( Archive )
20 Videos
Similar Questions
Knowledge Check
In isosceles triangle ABC, CA = CB = 4. which one of the following is the area of triangle ABC ?
A7B8C9DIt cannot be determined from the information givenThe ratio of the angles in ΔABC is 2 : 3 : 4. Which of the following triangles is similar to ΔABC ?
AΔDEF has angle in the ratio 4 : 3 : 2BΔPQR has angle in the ratio 1 : 2 : 3CΔLMN has angle in the ratio 1 : 1 : 1DΔMRQ has angle in the ratio 3 : 2 : 4
Which of the following hold(s) good for the function f(x)=2x−3x23 ∀x∈R?
View SolutionWhich of the following is true in a triangle ABC?
View SolutionWhich of the following relation(s) holds good for gaseous and reversible reactions?
View SolutionFor the following isomerisation reaction Cyclohexane ⇔ hexene -1, K = 1.732
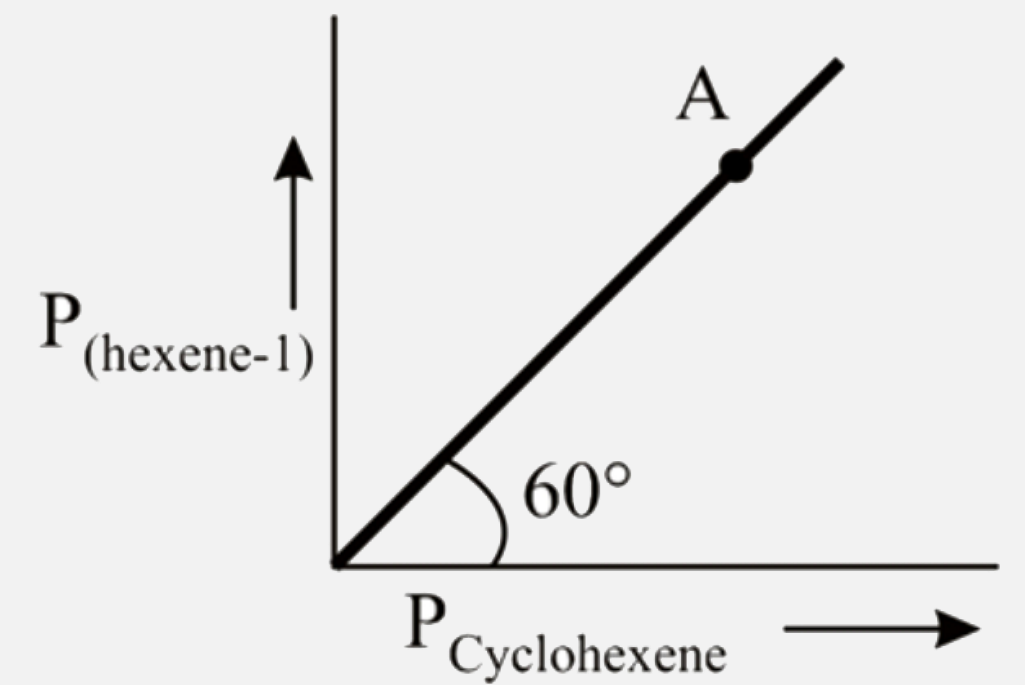
Which of the following statements holds good at point 'A' ?
View SolutionWhich one of the following inequality holds good:
View SolutionThe laws of reflection hold good for
View Solution
