which of the following graph represents the expression f(x)=ax2+bx+c (a≠0) when a>0,b<0 $ c<0 ?
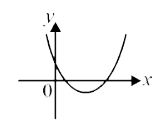
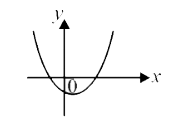
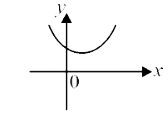

The correct Answer is:B
Step by step video & image solution for which of the following graph represents the expression f(x) = ax^2 + bx + c (a!=0) when a>0,b<0 $ c<0 ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONS & INEQUATIONS Book:VMC MODULES ENGLISHChapter:QUADRATIC EQUATIONS & INEQUATIONS Exercise:Numerical value type of JEE Main
Explore 15 Videos
- QUADRATIC EQUATIONS & INEQUATIONS Book:VMC MODULES ENGLISHChapter:QUADRATIC EQUATIONS & INEQUATIONS Exercise:JEE Main ( Archive )
Explore 20 Videos
- QUADRATIC EQUATIONS & INEQUATIONS Book:VMC MODULES ENGLISHChapter:QUADRATIC EQUATIONS & INEQUATIONS Exercise:JEE Advance ( Archive )
Explore 20 Videos
- PROPERTIES OF TRIANGLEBook:VMC MODULES ENGLISHChapter:PROPERTIES OF TRIANGLEExercise:JEE Advanced (Archive)
Explore 50 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:MATHEMATICS
Explore 30 Videos
Similar Questions
Knowledge Check
Each of the following graphs in the standard (x,y) coordinate plane has the same scale on both axes. One graph is the graph of ax+by≤c, where 0<a<b<c. Which one is it?
A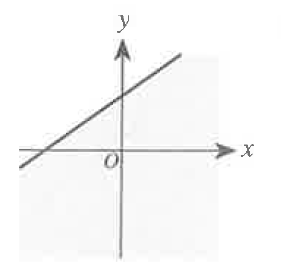 B
B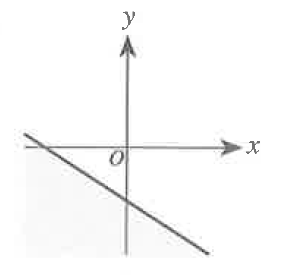 C
C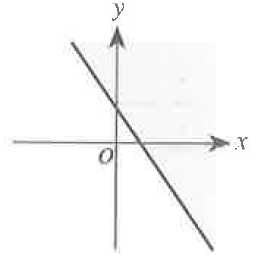 D
D
Which of the following statements are correct
E1) If a + b + c = 0 then 1 is a root of ax2+bx+c=0.
E2) If sinα,cosα are the roots of the equation ax2+bx+c=0 then b2−a2=2ac
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, find the signs of a,bandc.
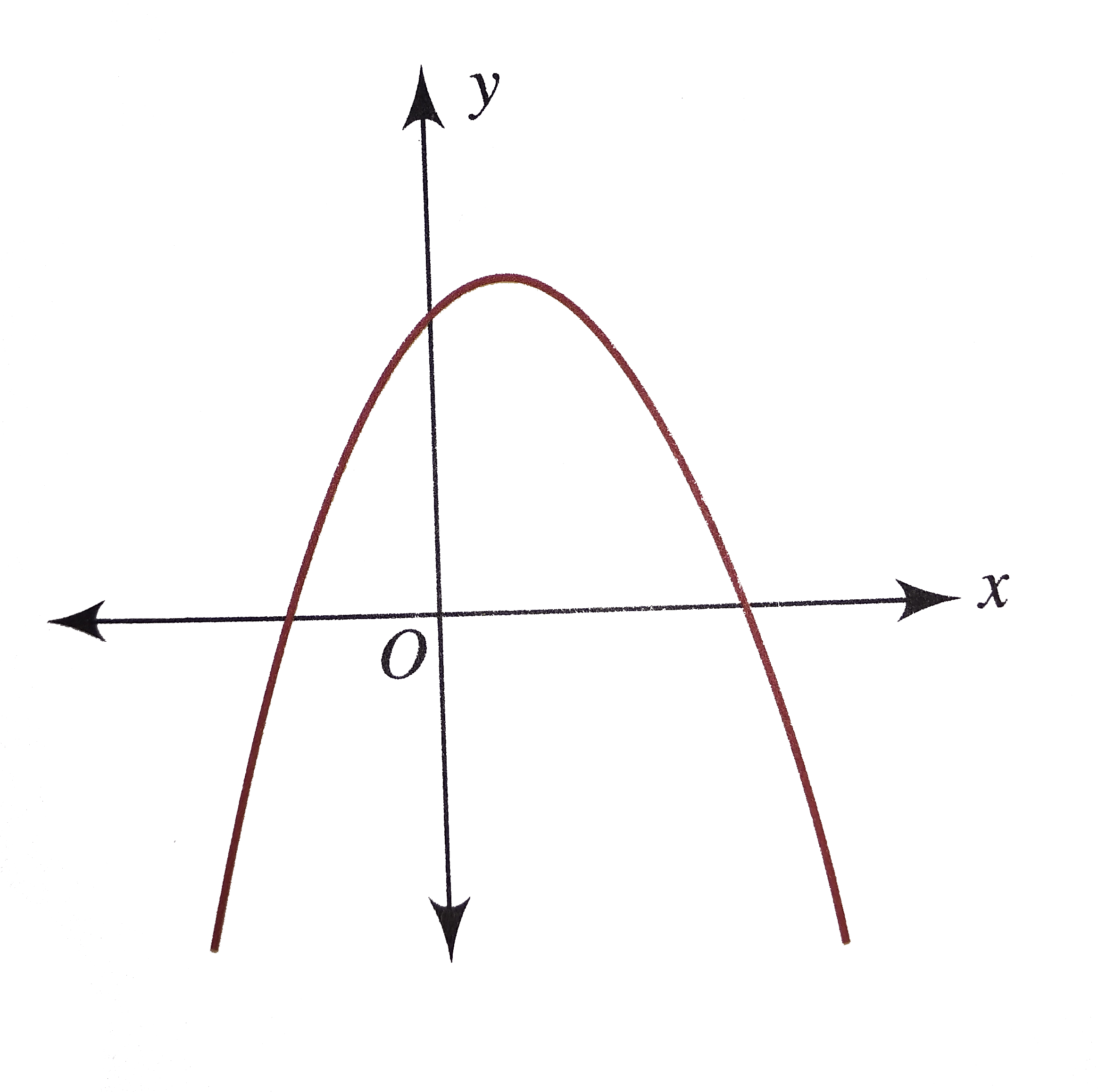
View SolutionThe following figure shows the graph of f(x)=ax2+bx+c, then find the sign of values of a,bandc.
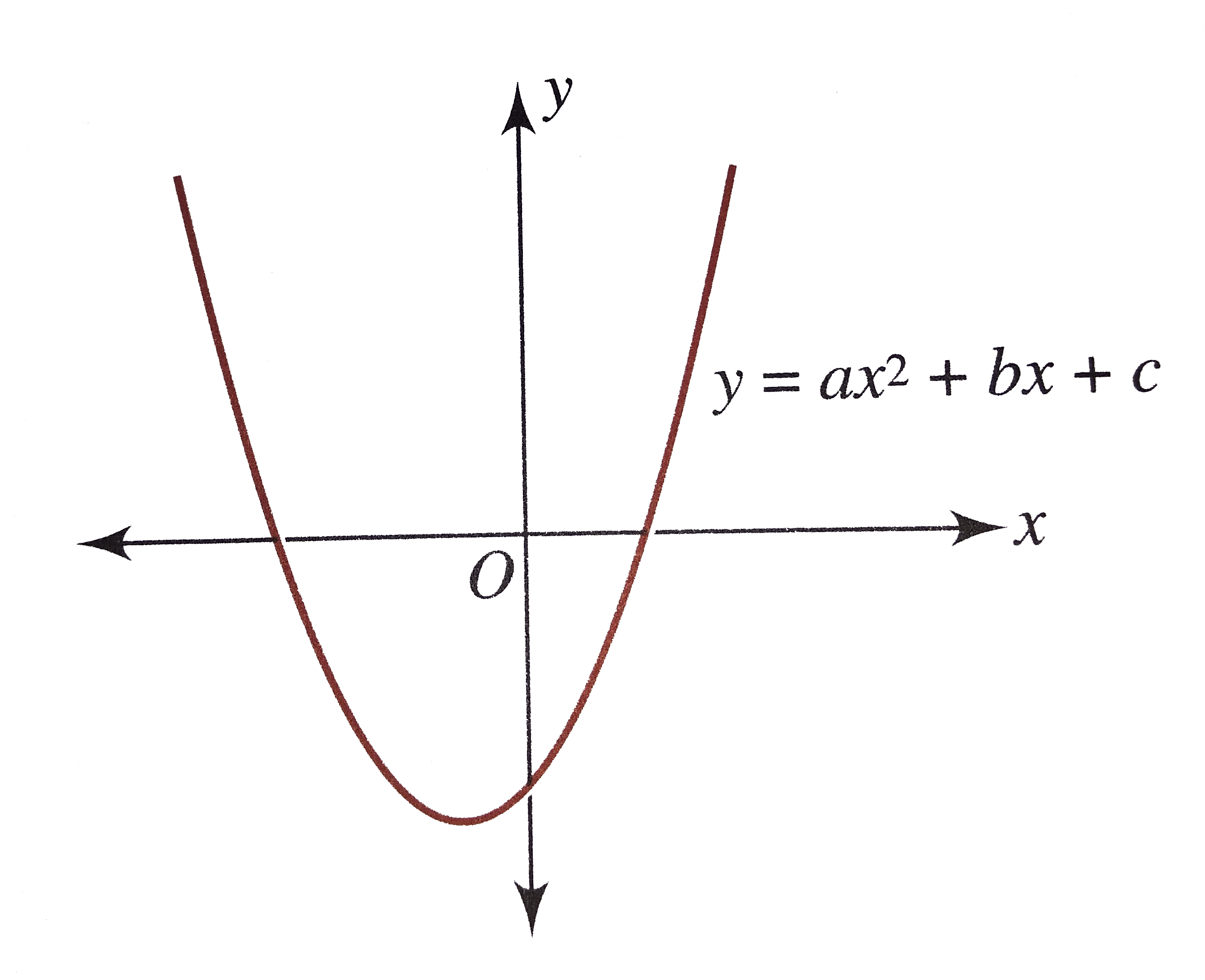
View SolutionFigure 2.23 show the graph of the polynomial f(x) = ax² + bx + c for which (a) a < 0, b > 0 and c > 0 (b) a < 0, b < 0 and c > 0 (c) a < 0, b < 0 and c < 0 (d) a > 0, b > 0 and c < 0
View SolutionThe quadratic expression ax2+bx+c>0∀x∈R, then :
View SolutionIf x2+ax+1 is a factor of ax3+bx+c, then which of the following conditions are not valid: a. a2+c=0 b. b−a=ac c. c3+c+b2=0 d. 2c+a=b
View SolutionEuler's substitution:
Integrals of the form ∫R(x,√ax2+bx+c)dx are claculated with the aid of one of the following three Euler substitutions:
i. √ax2+bx+c=t±x√aifa>0
ii. √ax2+bx+c=tx±x√cifc>0
iii. √ax2+bx+c=(x−a)tifax2+bx+c=a(x−a)(x−b) i.e., if α is real root of ax2+bx+c=0
xdx√7x−10−x23can be evaluated by substituting for x as
View Solution