If limx→a+f(x)=l=limx→a−g(x) and limx→a−f(x)=m=limx→a+g(x), the function f(x).g(x) is
is not continuous at x=a
has a limit when x→a and equal to lm
is continuous at x=a
has a limit when x→a and is not equal to lm
The correct Answer is:B
To solve the problem, we need to analyze the limits of the functions f(x) and g(x) as x approaches a from both sides.
1. Understanding the Given Limits:
We are given:
limx→a+f(x)=L=limx→a−g(x)
limx→a−f(x)=M=limx→a+g(x)
2. Finding the Left-Hand Limit of f(x)g(x):
We can express the limit of the product f(x)g(x) as:
limx→a−f(x)g(x)=limx→a−f(x)⋅limx→a−g(x)
From the given information, we know:
limx→a−f(x)=Mandlimx→a−g(x)=L
Therefore:
limx→a−f(x)g(x)=M⋅L
3. Finding the Right-Hand Limit of f(x)g(x):
Similarly, we can express the limit of the product as:
limx→a+f(x)g(x)=limx→a+f(x)⋅limx→a+g(x)
From the given information, we know:
limx→a+f(x)=Landlimx→a+g(x)=M
Therefore:
limx→a+f(x)g(x)=L⋅M
4. Equating the Two Limits:
Since both limits must be equal for the limit of the product to exist:
limx→a−f(x)g(x)=limx→a+f(x)g(x)
This gives us:
M⋅L=L⋅M
Hence, both limits are equal.
5. Conclusion:
Since the left-hand limit and right-hand limit are equal, we conclude that:
limx→af(x)g(x)=ML
Therefore, the function f(x)g(x) is continuous at x=a and has a limit equal to ML.
Final Answer:
The function f(x)g(x) has a limit as x→a and is equal to ML.
---
We are given:
limx→a+f(x)=L=limx→a−g(x)
limx→a−f(x)=M=limx→a+g(x)
We can express the limit of the product f(x)g(x) as:
limx→a−f(x)g(x)=limx→a−f(x)⋅limx→a−g(x)
From the given information, we know:
limx→a−f(x)=Mandlimx→a−g(x)=L
Therefore:
limx→a−f(x)g(x)=M⋅L
Similarly, we can express the limit of the product as:
limx→a+f(x)g(x)=limx→a+f(x)⋅limx→a+g(x)
From the given information, we know:
limx→a+f(x)=Landlimx→a+g(x)=M
Therefore:
limx→a+f(x)g(x)=L⋅M
Since both limits must be equal for the limit of the product to exist:
limx→a−f(x)g(x)=limx→a+f(x)g(x)
This gives us:
M⋅L=L⋅M
Hence, both limits are equal.
Since the left-hand limit and right-hand limit are equal, we conclude that:
limx→af(x)g(x)=ML
Therefore, the function f(x)g(x) is continuous at x=a and has a limit equal to ML.
The function f(x)g(x) has a limit as x→a and is equal to ML.
Topper's Solved these Questions
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - LEVEL 2
103 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - Numerical Value Type for JEE Main
14 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE
76 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
Similar Questions
If limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)g(x) limx→0(ax+bx+cx3)2x is equal to
View SolutionIf limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)g(x) limx→0(x−1+cosxx)1x is equal to
View SolutionIf limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)g(x)
limx→0(sinxx)sinxx−sinx is equal to
View SolutionIf limx→a[f(x)+g(x)]=2 and limx→a[f(x)−g(x)]=1, then find the value of limx→af(x)g(x).
View SolutionThe graph of y = f(x) is as shown in the following figure.
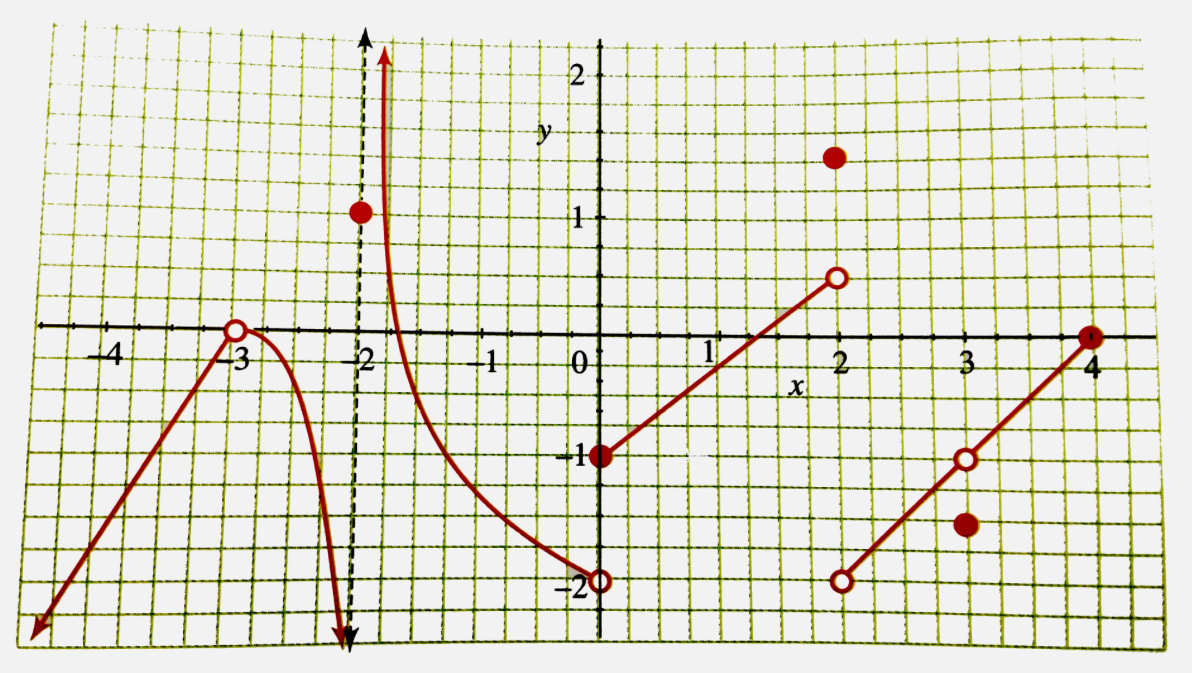
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f(x)=tanxx−π, then limx→(π)f(x)=……………….
View Solutionlimx→alog(x−a)log(ex−ea)
View SolutionLet f:R→R be a function given by f(x+y)=f(x)f(y)for all x,y∈R
If f(x)=1+xg(x)+x2g(x)ϕ(x)such that limx→0g(x)=aandlimx→0ϕ(x)=b, then f'(x) is equal to
View SolutionIf both Limx→c−f(x) and Limx→c+f(x) exist finitely and are equal, then the function f is said to have removable discontinuity at x=c. If both the limits i.e. Limx→c−f(x) and Limx→c+f(x) exist finitely and are not equal, then the function f is said to have non-removable discontinuity at x=c.
Which of the following function not defined at x=0 has removable discontinuity at the origin?
View SolutionIf limx→a(f(x)g(x)) exists, then
View Solution
