If y=f(x) and x=g(y) are inverse of each other. Then g'(y) and g(y) in terms of derivative of f(y) is
A.−f(x)[f'(x)]3
B. f(x)[f'(x)]2
C. −f(x)[f'(x)]2
D. None of these
−f(x)[f'(x)]3
f(x)[f'(x)]2
−f(x)[f'(x)]2
None of these
The correct Answer is:A
To solve the problem, we need to find g′(y) and g′′(y) in terms of the derivatives of f(x), given that y=f(x) and x=g(y) are inverse functions.
Step 1: Differentiate y=f(x)
We start by differentiating y=f(x) with respect to x:
dydx=f′(x)
Hint: Remember that the derivative of a function gives the slope of the tangent line at any point on the curve.
Step 2: Differentiate x=g(y)
Next, we differentiate x=g(y) with respect to y:
dxdy=g′(y)
Hint: This derivative represents how x changes with respect to y.
Step 3: Relate g′(y) and f′(x)
Since y=f(x) and x=g(y) are inverses, we know that:
dxdy=1dydx⟹g′(y)=1f′(x)
Hint: The relationship between the derivatives of inverse functions is key to solving this problem.
Step 4: Differentiate g′(y) to find g′′(y)
Now, we differentiate g′(y) with respect to y:
g′′(y)=ddy(1f′(x))
Using the chain rule, we get:
g′′(y)=−f′′(x)(f′(x))2⋅dxdy
Since dxdy=g′(y)=1f′(x), we substitute this into the equation:
g′′(y)=−f′′(x)(f′(x))2⋅1f′(x)=−f′′(x)(f′(x))3
Hint: When differentiating a quotient, remember to apply the quotient rule or the chain rule appropriately.
Conclusion
Thus, we have:
g′′(y)=−f′′(x)(f′(x))3
Final Answer
The correct option is:
A. −f′′(x)(f′(x))3
We start by differentiating y=f(x) with respect to x:
dydx=f′(x)
Next, we differentiate x=g(y) with respect to y:
dxdy=g′(y)
Since y=f(x) and x=g(y) are inverses, we know that:
dxdy=1dydx⟹g′(y)=1f′(x)
Now, we differentiate g′(y) with respect to y:
g′′(y)=ddy(1f′(x))
Using the chain rule, we get:
g′′(y)=−f′′(x)(f′(x))2⋅dxdy
Since dxdy=g′(y)=1f′(x), we substitute this into the equation:
g′′(y)=−f′′(x)(f′(x))2⋅1f′(x)=−f′′(x)(f′(x))3
Thus, we have:
g′′(y)=−f′′(x)(f′(x))3
The correct option is:
A. −f′′(x)(f′(x))3
Topper's Solved these Questions
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - Numerical Value Type for JEE Main
14 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE main (Archive)
51 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - LEVEL -1
134 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE ADVANCED ARCHIVE
76 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
Similar Questions
If y=f(x)andx=g(y) are inverse functions of each other, then
View SolutionIf y=f(x)=x3+x5 and g is the inverse of f find g′(2)
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionGraph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
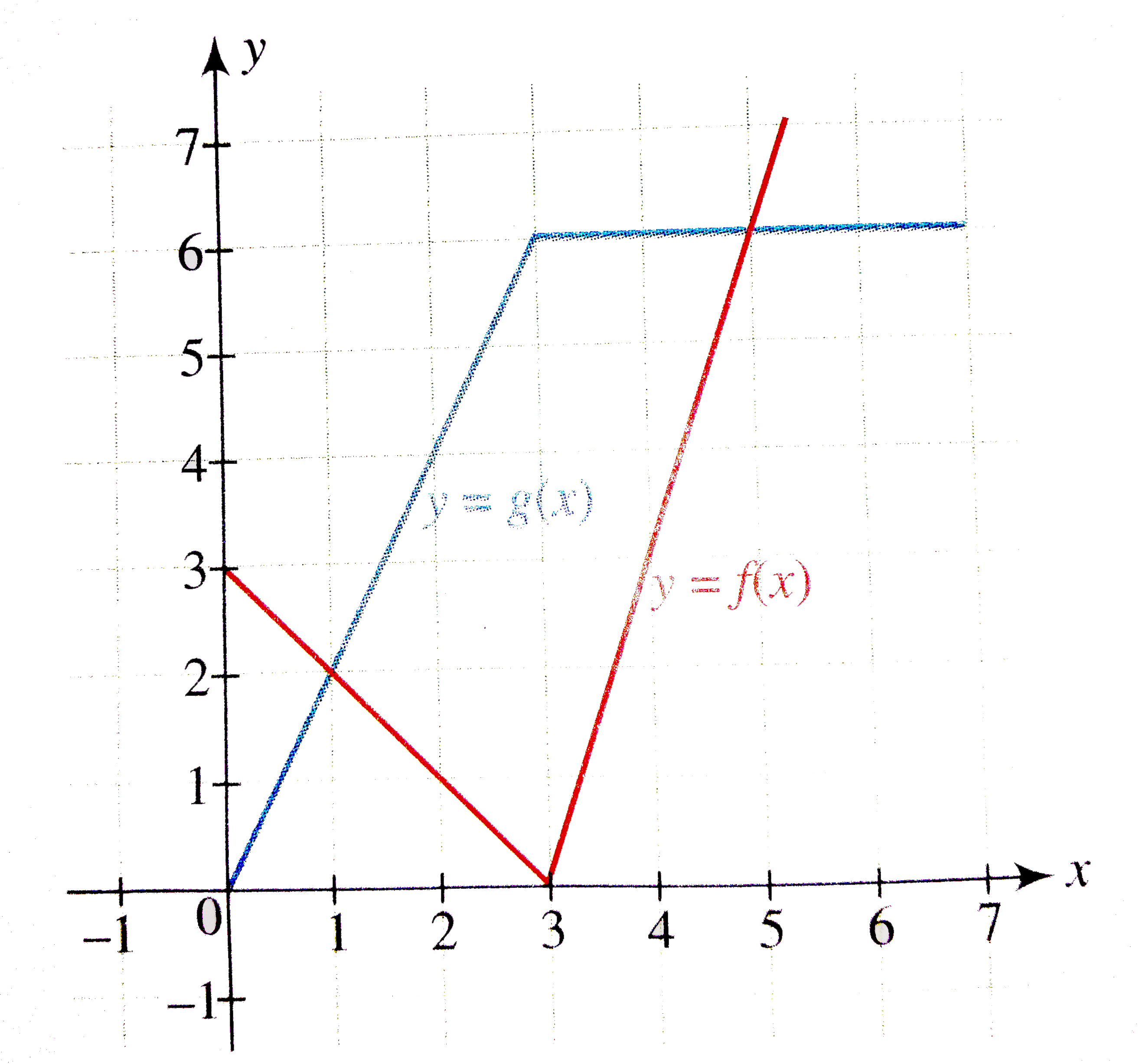
View SolutionGiven the function f(x)=ax+a−x2(wherea>2).Thenf(x+y)+f(x−y)= 2f(x).f(y) (b) f(x).f(y) f(x)f(y) (d) none of these
View SolutionIf f(x−y),f(x)f(y),andf(x+y) are in A.P. for all x, y, and f(0)≠0, then
View SolutionIf f(x−y),f(x)f(y),andf(x+y) are in A.P. for all x, y, and f(0)≠0, then
View SolutionIf g is inverse of f then prove that f''(g(x))=−g''(x)(f'(g(x)))3.
View SolutionIf g is inverse of f then prove that f''(g(x))=−g''(x)(f'(g(x)))3.
View Solution
