In a submarine telegraph cable the speed of signaling varies as where is the ratio of the radius of the cable to that of covering. Then the greatest speed is attained when this ratio is
To find the ratio x at which the greatest speed of signaling in a submarine telegraph cable is attained, we start with the given relationship for speed:
s∝x2log(1x)
This can be expressed as:
s=k⋅x2log(1x)
where k is a constant.
Step 1: Differentiate the speed function with respect to x
To find the maximum speed, we need to differentiate s with respect to x and set the derivative equal to zero:
dsdx=ddx(k⋅x2log(1x))
Using the product rule, we differentiate:
dsdx=k(ddx(x2)⋅log(1x)+x2⋅ddx(log(1x)))
Step 2: Calculate the derivatives
1. The derivative of x2 is:
ddx(x2)=2x
2. The derivative of log(1x) using the chain rule is:
ddx(log(1x))=ddx(−log(x))=−1x
Step 3: Substitute the derivatives back into the equation
Now substituting these derivatives back into our expression for dsdx:
dsdx=k(2x⋅log(1x)+x2⋅(−1x))
This simplifies to:
dsdx=k(2xlog(1x)−x)
Step 4: Set the derivative to zero
Setting dsdx=0:
k(2xlog(1x)−x)=0
Since k≠0, we can simplify to:
2xlog(1x)−x=0
Step 5: Factor out x
Factoring out x:
x(2log(1x)−1)=0
This gives us two cases:
1. x=0 (not valid in this context)
2. 2log(1x)−1=0
Step 6: Solve for x
From the second case:
2log(1x)=1
This simplifies to:
log(1x)=12
Exponentiating both sides gives:
1x=e12⟹x=1√e
Step 7: Express the ratio
Thus, the ratio x is:
x=1√e⟹Ratio=1:√e
Final Answer
The greatest speed is attained when the ratio x is:
1:√e
2. 2log(1x)−1=0
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Level -269videos
DIFFERENTIAL CALCULUS 2
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Numerical ValueType for JEE Main14videos
DIFFERENTIAL CALCULUS 2
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)81videos
DIFFERENTIAL CALCULUS 2
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)75videos
DIFFERENTIAL CALCULUS
- BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )32videos
DIFFERENTIAL EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If y varies directly as x and y=12, where x=c, what is y in terms of c when x=8?
A2c3B32cC20cD96c - Question 2 - Select One
The earth moves around the Sun in an elliptical orbit as shown in Fig. The ratio OA/OB=x. The ratio of the speed of the earth at B to that at A is nearly
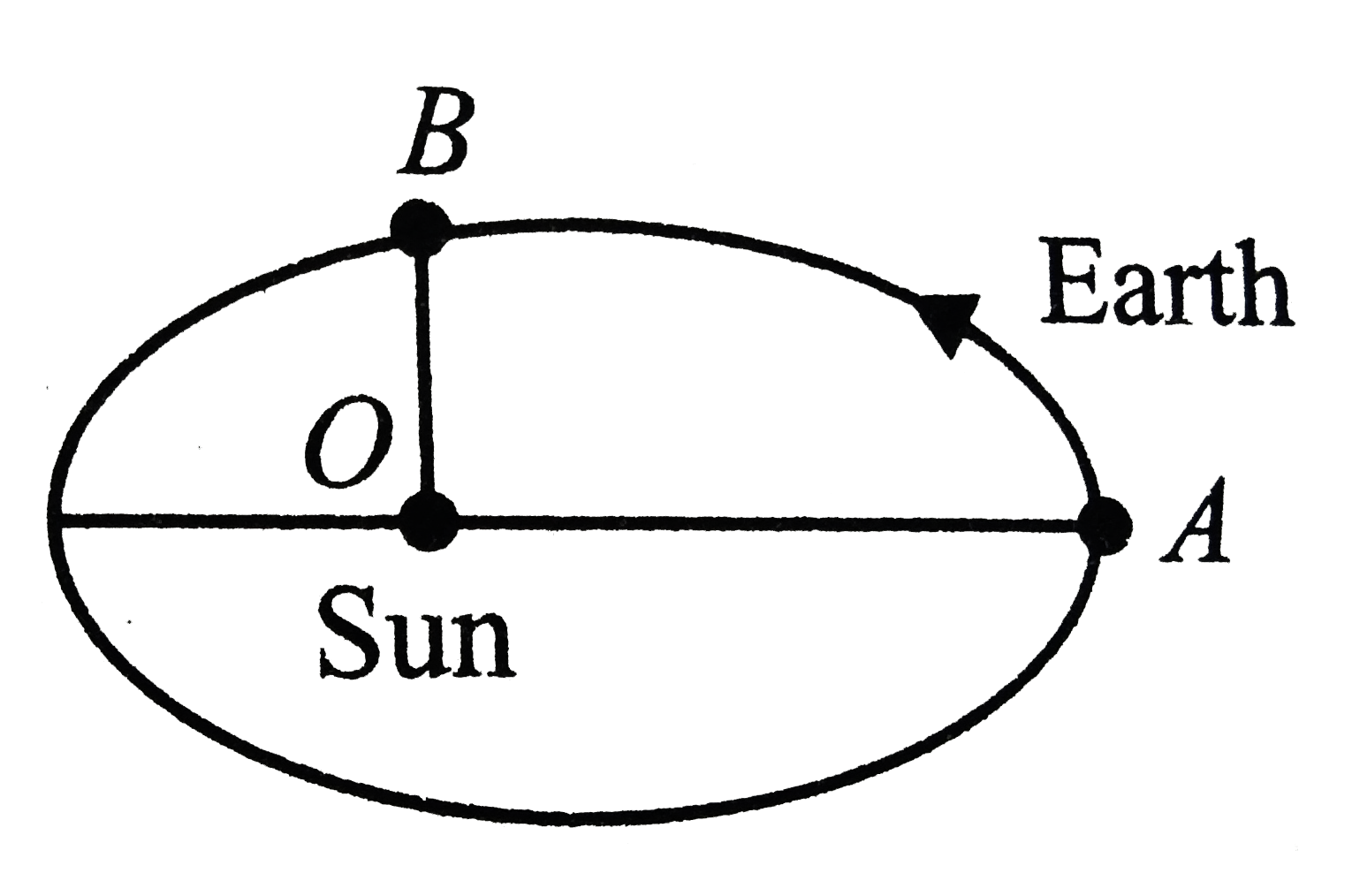 A√xBxCx√xDx2
A√xBxCx√xDx2
The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
View SolutionFind the domain of the function f(x)=loge(x−[x]), where [.] denotes the greatest integer function.
View SolutionThe equation of a travelling sound wave is y=6.0sin(600t−1.8x) where y is measured in 10−5m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
View SolutionFind the domain and range of f(x)=log[cos|x|+12],where [.] denotes the greatest integer function.
View SolutionA flexible steel cable of total length L and mass per unit length μ hangs vertically from a support at one end. (a) Show that the speed of a transverse wave down the cable is v=√g(L−x), where x is measured from the support. (b) How long will it takes for a wave to travel down the cable?
View Solutionf(x)=log(x−[x]), where [⋅] denotes the greatest integer function. find the domain of f(x).
View Solution

