A lizard, at an initial distance of 21 cm behind an insect, moves from rest with an acceleration of 2cms−2 and pursues the insect which is crawling uniformly along a straight line at a speed of 20cms−1. Then the lizard will catch the insect after
(a) 24 s
(b) 21 s
(c) 1 s
(d) 20 s
The correct Answer is:B
To solve the problem, we need to find out how long it takes for the lizard to catch the insect. We will use the equations of motion for both the lizard and the insect.
1. Identify the Given Information:
- Initial distance between the lizard and the insect, d=21cm
- Acceleration of the lizard, aL=2cm/s2
- Speed of the insect, vI=20cm/s
2. Write the Equation of Motion for the Lizard:
The lizard starts from rest, so its initial velocity uL=0. The distance covered by the lizard after time t is given by:
SL=uLt+12aLt2=0+12(2)t2=t2
Thus, the distance covered by the lizard is:
SL=t2
3. Write the Equation of Motion for the Insect:
The insect is moving at a constant speed, so its distance covered after time t is:
SI=vIt=20t
4. Set Up the Equation:
Since the lizard is initially 21 cm behind the insect, the distance covered by the lizard must equal the distance covered by the insect plus the initial distance:
SL=SI+21
Substituting the expressions for SL and SI:
t2=20t+21
5. Rearrange the Equation:
Rearranging gives us a standard quadratic equation:
t2−20t−21=0
6. Solve the Quadratic Equation:
We can use the quadratic formula t=−b±√b2−4ac2a, where a=1,b=−20,c=−21:
t=20±√(−20)2−4⋅1⋅(−21)2⋅1
t=20±√400+842
t=20±√4842
t=20±222
7. Calculate the Possible Values for t:
- Positive root:
t=422=21s
- Negative root:
t=−22=−1s(not valid since time cannot be negative)
8. Conclusion:
The lizard will catch the insect after t=21s.
Final Answer:
The lizard will catch the insect after 21 seconds.
- Initial distance between the lizard and the insect, d=21cm
- Acceleration of the lizard, aL=2cm/s2
- Speed of the insect, vI=20cm/s
The lizard starts from rest, so its initial velocity uL=0. The distance covered by the lizard after time t is given by:
SL=uLt+12aLt2=0+12(2)t2=t2
Thus, the distance covered by the lizard is:
SL=t2
The insect is moving at a constant speed, so its distance covered after time t is:
SI=vIt=20t
Since the lizard is initially 21 cm behind the insect, the distance covered by the lizard must equal the distance covered by the insect plus the initial distance:
SL=SI+21
Substituting the expressions for SL and SI:
t2=20t+21
Rearranging gives us a standard quadratic equation:
t2−20t−21=0
We can use the quadratic formula t=−b±√b2−4ac2a, where a=1,b=−20,c=−21:
t=20±√(−20)2−4⋅1⋅(−21)2⋅1
t=20±√400+842
t=20±√4842
t=20±222
- Positive root:
t=422=21s
- Negative root:
t=−22=−1s(not valid since time cannot be negative)
The lizard will catch the insect after t=21s.
The lizard will catch the insect after 21 seconds.
Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Advanced (Archive)
81 Videos
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - Numerical ValueType for JEE Main
14 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- DIFFERENTIAL EQUATIONSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )
32 Videos
Similar Questions
The displacement of a body in 8 s starting from rest with an acceleration of 20cms−2 is
View SolutionA scooter starts from rest have an acceleration of 1ms−2 while a car 150 m behind it starts from rest with an acceleration of 2ms−2. After how much time the car catches up with the scooter ?
View Solution
Knowledge Check
How long would it take a car, starting from rest and accelerating uniformly in a straight line at 5m/s2, to cover a distance of 200 m ?
A9.0 sB10.5 sC12.0 sD15.5 sWhen an object is kept at a distance of 30cm from a concave mirror, the image is formed at a distance of 10 cm. If the object is moved with a speed of 9ms−1 the speed with which the image moves is
A10ms−1B1ms−1C9ms−1D0.9ms−1
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View SolutionA bus starting from rest moves with a uniform acceleration of 0.1m/s2 for 2 minutes. Find
(a) the speed acquired, (b) the distance travelled.
View SolutionWhen an object is kept at a distance of 30cm from a concave mirror, the image is formed at a distance of 10 cm. If the object is moved with a speed of 9cms−1 the speed with which the image moves is
View SolutionA plane mirror is placed with its plane at an angle 30∘ with the y-axis. Plane of the mirror is perpendicular to the xy-plane and the length of the mirror is 3m. An insect moves along x-axis starting from a distant point, with speed 2 cm/s. The duration of the time for which the insect can see its shown image in the mirror is:
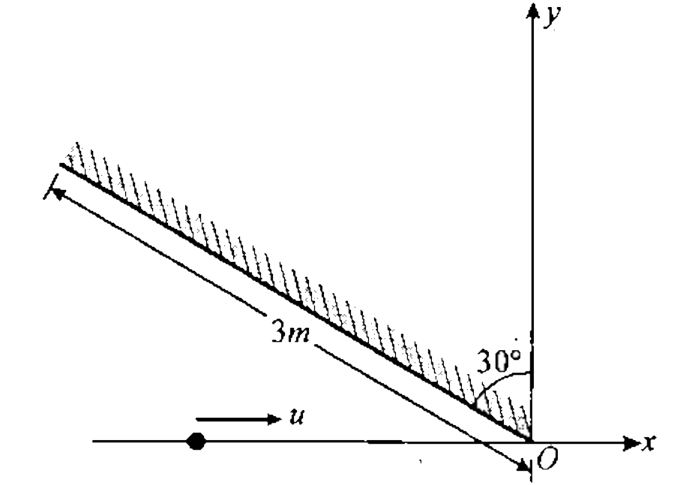
View SolutionA particle is executing S.H.M. from mean position at 5 cm distance, acceleration is 20cm/sec2 then value of angular velocity will be
View SolutionA car is standing 200m behind a bus , which is also at rest . The two. Start moving at the same instant but with different forward accelerations. The bus has acceleration 2ms−2 and The car has acceleration 4ms−2 The car will catch up will the bus after time :
View Solution
