Using the relation 2(1−cosx)<x2 ,x=0 or prove that sin(tanx)≥x,∀ϵ[0,π4]
Step by step video & image solution for Using the relation 2(1−cosx)<x^2 ,x=0 or prove that sin(tanx)≥x,∀ϵ[0,π/4] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL CALCULUS 2BOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUS 2EXERCISE - JEE Main (Archive)
36 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
- DIFFERENTIAL EQUATIONSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - JEE ADVANCE (ARCHIVE )
32 Videos
Similar Questions
The number of solutions of the equation secx1−cosx=11−cosx in [0, 2π] is equal to 3 (b) 2 (c) 1 (d) 0
View SolutionSolutions of the equations (2cosx−1)(3cosx+4)=0 is [0,2π] is:
View SolutionIntegrate the functions1−cosx1+cosx
View SolutionIntegrate the functionscosx1+cosx
View SolutionUsing constraint method find the relation between accelerations of 1 and 2.
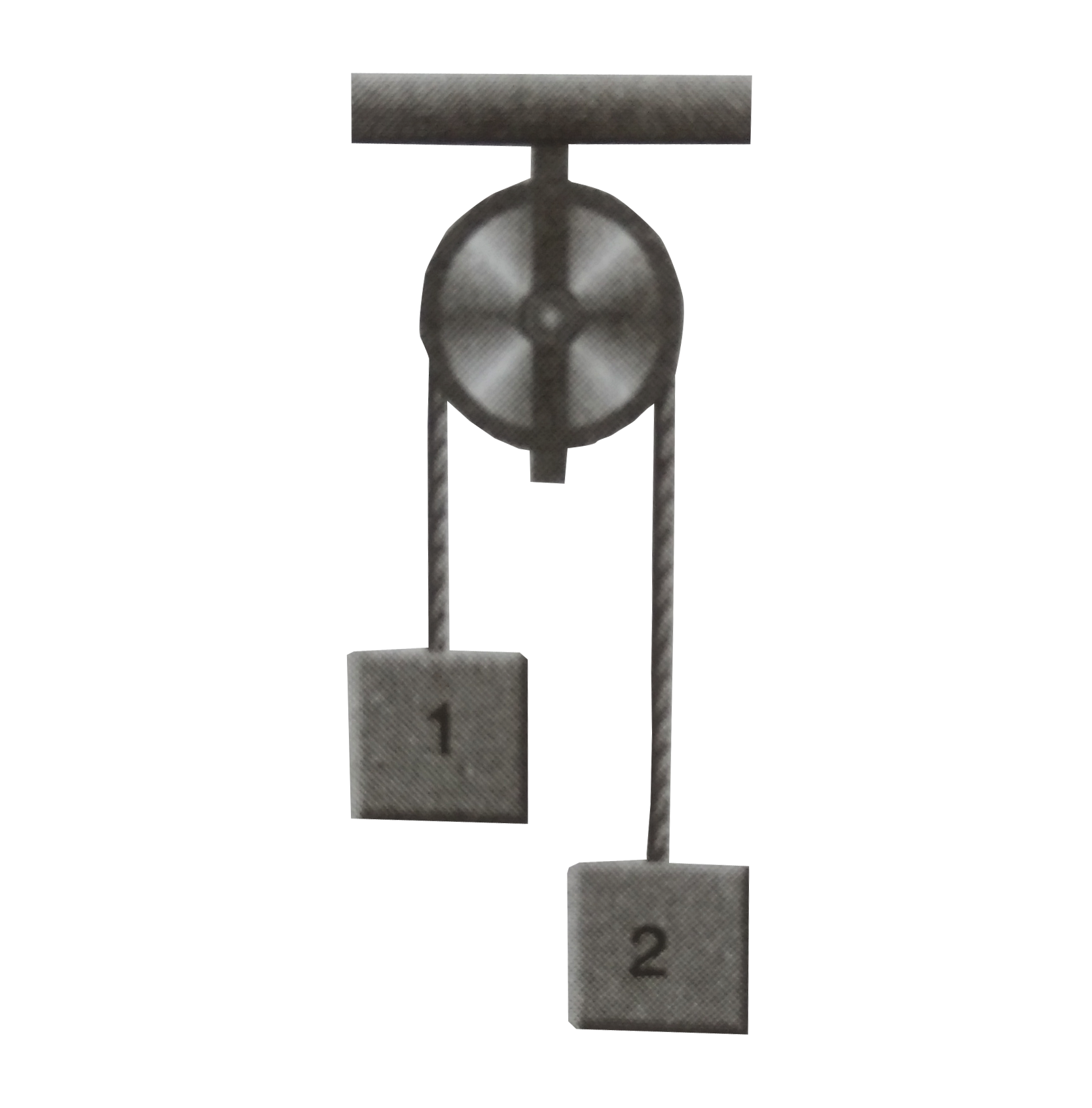
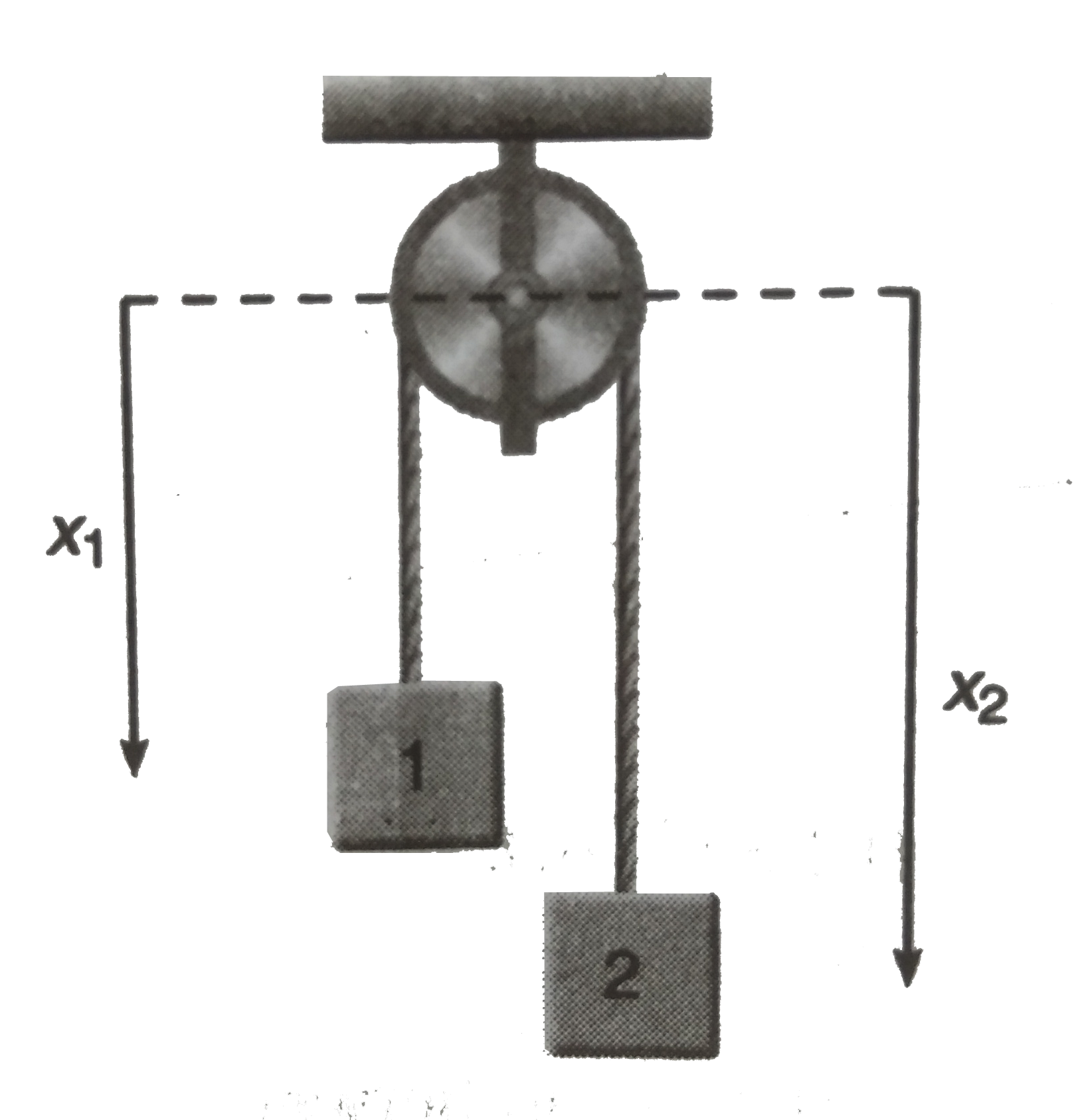
View SolutionUsing constraint method find the relation between of a1 and a2.

View SolutionUsing contraint equation. Find the relation between a1anda2.
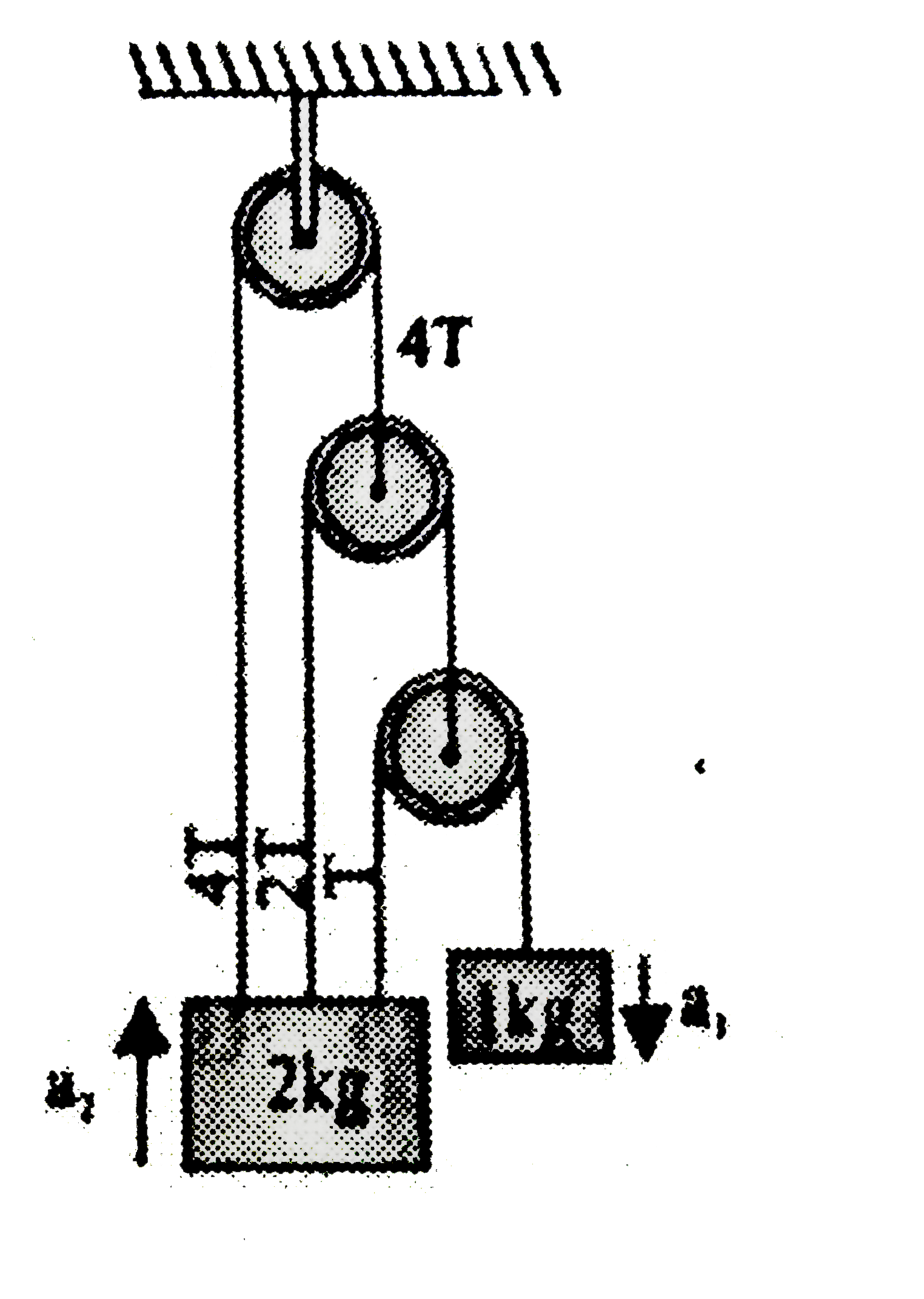
View SolutionFind the solution of cosx=12.
View SolutionIf x1,x2,...,xn are real numbers, then the largest value of the expression
sinx1cosx2+sinx2cosx3+...+sinxncosx1, is
View Solutionsolve equation 2tan−1(cosx)=tan−1(2cosecx)
View Solution
