Find area parallelogram lines y=mx,y=mx+1,y=nxandy=nx+1 equal to:
The correct Answer is:1/|m-n|
To find the area of the parallelogram formed by the lines y=mx, y=mx+1, y=nx, and y=nx+1, we can follow these steps:
Step 1: Identify the lines and their intersections
The lines given are:
1. y=mx
2. y=mx+1
3. y=nx
4. y=nx+1
We need to find the points of intersection of these lines to determine the vertices of the parallelogram.
Step 2: Find the intersection points
To find the intersection of the lines y=mx and y=nx+1:
Set mx=nx+1.
Rearranging gives:
mx−nx=1⟹(m−n)x=1⟹x=1m−n
Substituting x back into y=mx:
y=m(1m−n)=mm−n
Thus, one vertex A is (1m−n,mm−n).
Next, find the intersection of the lines y=mx+1 and y=nx:
Set mx+1=nx.
Rearranging gives:
mx−nx=−1⟹(m−n)x=−1⟹x=−1m−n
Substituting x back into y=mx+1:
y=m(−1m−n)+1=−mm−n+1=−m+(m−n)m−n=nm−n
Thus, another vertex B is (−1m−n,nm−n).
Step 3: Calculate the area of the parallelogram
The area A of the parallelogram can be calculated using the formula:
A=base×height
Here, the base can be taken as the distance between the lines y=mx and y=mx+1, which is 1. The height is the distance between the lines y=nx and y=mx.
The height can be calculated as:
Height=1|m−n|
Thus, the area of the parallelogram is:
A=base×height=1×1|m−n|=1|m−n|
Final Answer
The area of the parallelogram is:
Area=1|m−n|
The lines given are:
1. y=mx
2. y=mx+1
3. y=nx
4. y=nx+1
To find the intersection of the lines y=mx and y=nx+1:
Set mx=nx+1.
Rearranging gives:
mx−nx=1⟹(m−n)x=1⟹x=1m−n
Substituting x back into y=mx:
y=m(1m−n)=mm−n
Thus, one vertex A is (1m−n,mm−n).
Set mx+1=nx.
Rearranging gives:
mx−nx=−1⟹(m−n)x=−1⟹x=−1m−n
Substituting x back into y=mx+1:
y=m(−1m−n)+1=−mm−n+1=−m+(m−n)m−n=nm−n
Thus, another vertex B is (−1m−n,nm−n).
The area A of the parallelogram can be calculated using the formula:
A=base×height
Here, the base can be taken as the distance between the lines y=mx and y=mx+1, which is 1. The height is the distance between the lines y=nx and y=mx.
Height=1|m−n|
Thus, the area of the parallelogram is:
A=base×height=1×1|m−n|=1|m−n|
The area of the parallelogram is:
Area=1|m−n|
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - NUMERICAL VALUE TYPE FOR JEE MAIN
14 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - JEE MAIN (ARCHIVE)
87 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - LEVEL-1
90 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Archive (State true or false: Q. 42)
1 Videos
- TRIGONOMETRIC IDENTITIES AND EQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - TRIGONOMETRIC IDENTITIES AND EQUATIONS EXERCISE - JEE Advanced (Archive)
11 Videos
Similar Questions
Find the value of m so that lines y=x+1,2x+y=16andy=mx−4 may be concurrent.
View SolutionIf the lines represented by 2x2−5xy+2y2=0 be the sides of a parallelogram and the line 5x+2y=1 be one of its diagonal. Find the equation of the other diagonal, and area of the parallelogram .
View SolutionFind the area bounded by the parabola x2=y and line y=1.
View SolutionFor what value of m are the three lines y=x+1,y=2(x+1)andy=mx+3 concurrent ?
View SolutionLet m be a positive integer and let the lines 13x+11y=700 and y=mx−1 intersect in a point whose coordinates are integer. Then m equals to :
View SolutionFind the perpendicular distance between the lines
y=mx+c,y=mx+d
View Solution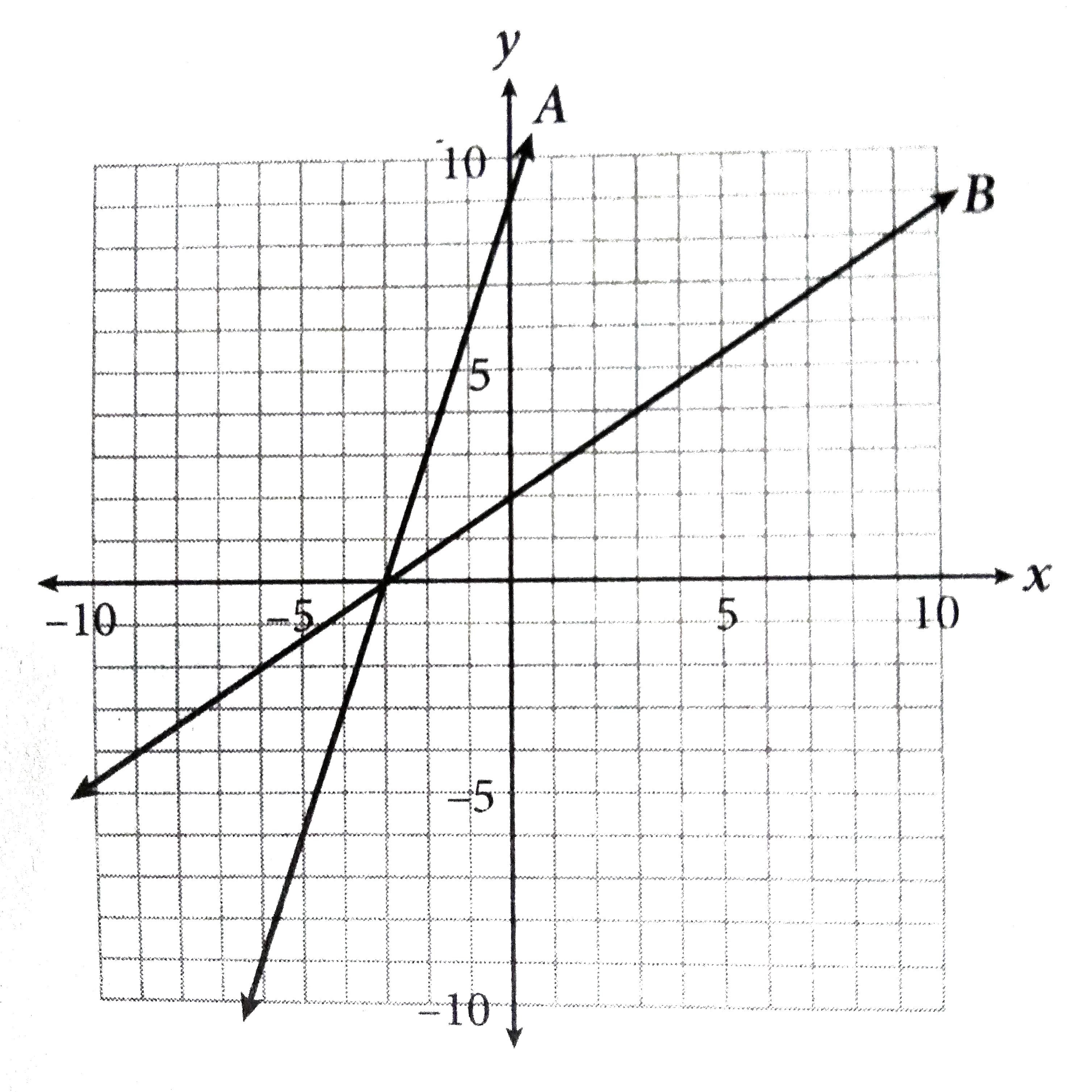
If the equation of line A shown on the graph is given by y=mx+b, and the equation of line B is given by y=k(mx+b), what is the value of k?
View SolutionFind the value of m, for which the line y=mx+25√33 is a normal to the conic x216−y29=1.
View SolutionThe distance between the lines y=mx+c1 and y=mx+c2 is
View SolutionFor positive l, m and n, if the points x=ny+mz,y=lz+nx,z=mx+ly intersect in a straight line, when
Q. l, m and n satisfy the equation
View Solution
