A line with positive direction cosines passes through the point P(2,−1,2) and makes equal angles with the coordinate axes. The line meets the plane 2x+y+z=9 at point Q. Find the length of the line segment PQ.
1
√2
√3
2
The correct Answer is:C
Step by step video & image solution for A line with positive direction cosines passes through the point P(2, -1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x+y+z= 9 at point Q. Find the length of the line segment PQ. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - JEE MAIN (ARCHIVE)
87 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Archive (State true or false: Q. 42)
1 Videos
- TRIGONOMETRIC IDENTITIES AND EQUATIONS BOOK - VMC MODULES ENGLISHCHAPTER - TRIGONOMETRIC IDENTITIES AND EQUATIONS EXERCISE - JEE Advanced (Archive)
11 Videos
Similar Questions
A line with positive direction cosines passes through the point P(2, – 1, 2) and makes equal angles with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals
View SolutionA line with positive direction cosines passes through the point P(2,–1,2) and makes equal angles with the coordinate axes. The line meets the plane 2x+y+z=9 at point Q. The length of the line segment PQ equals
View SolutionFind the direction cosines of the line passing through two points
View SolutionFind the direction cosines of a line which makes equal angles with the coordinate axes.
View SolutionFind the direction cosines of the line passing through the two points (2,4,5)and (1,2,3).
View SolutionFind the direction cosines of the line passing through the two points (-1, 2, 3) and (2, -3, 5).
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
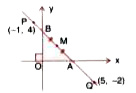
The equation of the line.
View SolutionFind the equation of the lines through the point (3, 2) which make an angle of 45 with the line x−2y=3 .
View SolutionFind the equation of the lines through the point (3, 2) which make an angle of 45∘with the line x−2y=3.
View SolutionThe direction cosines of the line passing through P(2,3,−1) and the origin are
View Solution
