Following results are observed when sodium metal is irradiated with different wavelength. Calculate (a) threshold wavelength and (b) Planck's constant
λ(nm)500450400v×10−5(cms−1)2.554.355.35
Suppose threshold wavelength =λ0nm=λ0×10−9m
Also, h(v−v0)=12mv2 or hc(1λ−1λ0)=12mv2
Substituting the given results of the three experiments, we get
hc10−9(1500−1λ0)=12m(2.55×106)2 ...(A)
hc10(−9)(1450−1λ0)=12m(4.35×106)2 ...(B)
hc10−9(1400−1λ0)=12m(5.20×106)2 ....(C)
Dividing eqn.(B) by eqn. (A), we get
Or λ0−450λ−500×450500=(4.352.55)2=2.910 or λ0−450=2.619λ0−1309.5
Or 1.619λ0=8.596∴λ0=531nm Substituting this value in eqn. (C), we get
h×(3×108)10−9(1400−1531)=12(9.11×10−31)(5.20×106)2 or h=6.66×10−34Js
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 1
75 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 2
50 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - 0 (Short Answer Type-II (3 Marks))
6 Videos
- AMINESBOOK - VMC MODULES ENGLISHCHAPTER - AMINESEXERCISE - IN CHAPTER EXERCISE H
10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL BONDING & CHEMICAL STRUCTURE EXERCISE - IMPECCABLE
50 Videos
Similar Questions
Knowledge Check
Calculate the energy in joule corresponding to light of wavelength 45 nm : (Planck's constant h=6.63×10−34 Js: speed of light :c=3×108ms−1).
A6.67×1015B6.67×1011C4.42×10−15D4.42×10−18
When a metallic surface is illuminated with radiation of wavelength λ, the stopping potential is V. If the same surface is illuminated with radiation of wavelength 2λ , the stopping potential is V4. The threshold wavelength surface is :
(a) 5λ (b) 52λ (c) 3λ (d) 4λ
View SolutionThe work function for tungsten and sodium are 4.5eV and 2.3eV respectively . If the threshold wavelength λ for sodium is 5460Å, the value of λ for tungsten is
View SolutionThe frequency of the strong yellow line in the spectrum of sodium in 5.09×1014s−1 .Calculate the wavelength of the light nanometres
View SolutionIn an experiment on photoelectric effect, the stopping potential is measured for monochromatic light beams corresponding to different wavelength. The data collected are as follows:
wavelength (nm): 350 400 450 500 550
stopping potential (V): 1.45 1.00 0.66 0.38 0.16
Plot the stopping potential against inverse of wavelength on a graph paper and find (a) the Planck constant, (b) the work function of the emitter and (c) the threshold wavelength .
View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
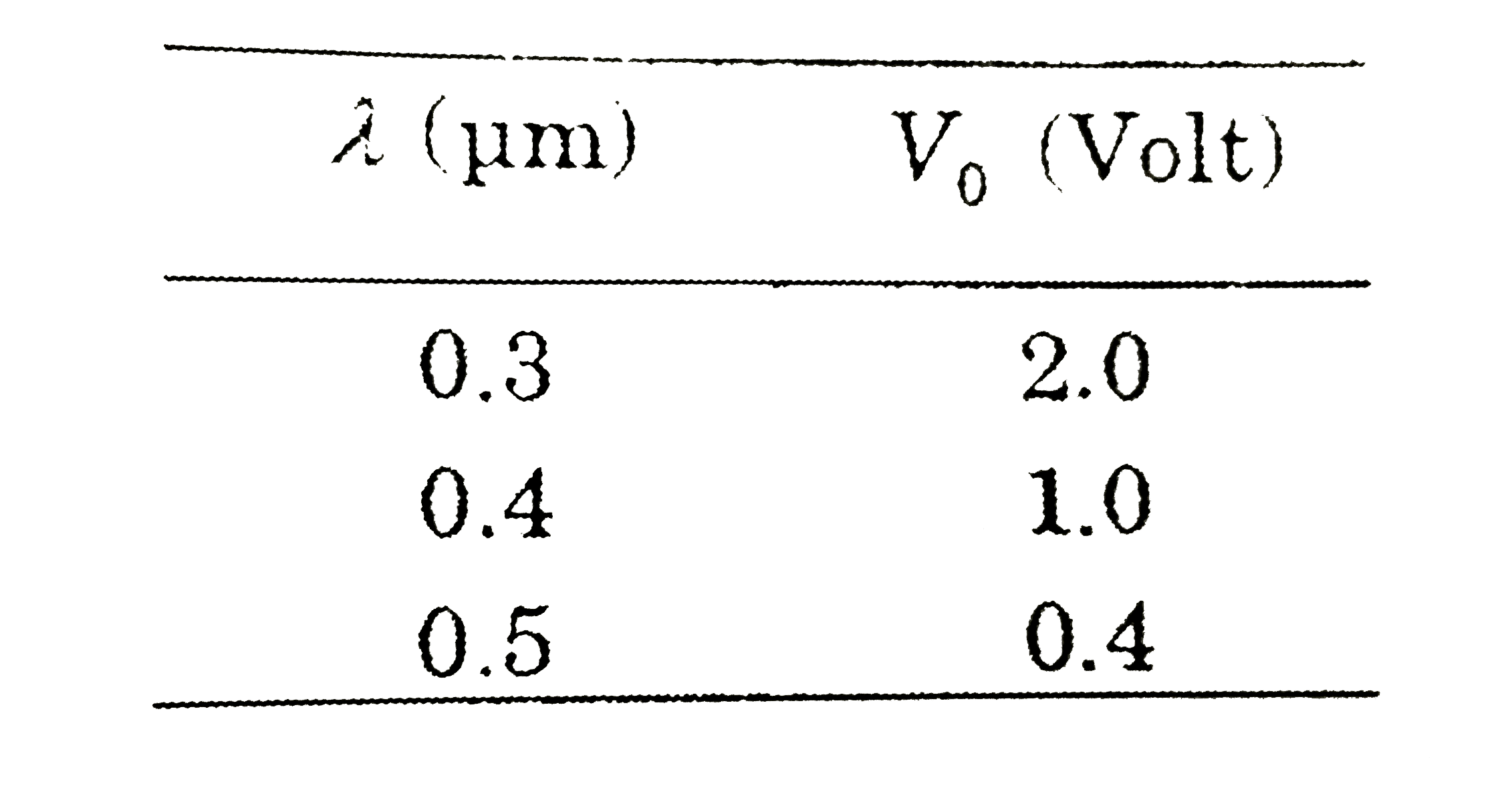
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is
View SolutionA slit 5 cm wide when irradiated by waves of wavelength 10 mm results in the angular spread of the central maxima on either side of incident light by about :
View SolutionThe work function of a metal is in the range of 2 eV to 5 eV. Find which of the following wavelength of light cannot be used for photoelectric effect. (Consider, Planck's constant =4×10−15 eV - s, velocity of light =3×108ms−1)
View Solution
