To which quantum level does the electron jump in H atom from the lowest level if it is given an energy corresponding to 99% of the ionization potential of hydrogen atom?
The correct Answer is:10
To solve the problem of determining to which quantum level an electron in a hydrogen atom jumps when given energy corresponding to 99% of the ionization potential, we can follow these steps:
1. Understand Ionization Energy: The ionization potential (or ionization energy) of the hydrogen atom is the energy required to remove the electron from the ground state (n=1) to infinity (n=∞). The ionization energy of hydrogen is approximately 13.6 eV.
2. Calculate 99% of Ionization Energy:
Energy given=0.99×Ionization Energy=0.99×13.6eV=13.464eV
3. Use the Energy Level Formula: The energy of an electron in a hydrogen atom at quantum level n is given by:
En=−E0n2
where E0=13.6eV.
4. Set Up the Equation: The energy difference when the electron jumps from level n1 (where n1=1) to level n2 can be expressed as:
E=En2−En1=−E0n22−(−E012)=E0(1−1n22)
5. Substitute the Given Energy: We know that the energy given is 99% of the ionization energy, so we set:
13.464=13.6(1−1n22)
6. Solve for n2:
- Divide both sides by 13.6:
13.46413.6=1−1n22
- Calculate 13.46413.6:
0.99=1−1n22
- Rearranging gives:
1n22=1−0.99=0.01
- Taking the reciprocal gives:
n22=100
- Taking the square root gives:
n2=10
Final Answer:
The electron jumps to the quantum level n=10.
Energy given=0.99×Ionization Energy=0.99×13.6eV=13.464eV
En=−E0n2
where E0=13.6eV.
E=En2−En1=−E0n22−(−E012)=E0(1−1n22)
13.464=13.6(1−1n22)
- Divide both sides by 13.6:
13.46413.6=1−1n22
- Calculate 13.46413.6:
0.99=1−1n22
- Rearranging gives:
1n22=1−0.99=0.01
- Taking the reciprocal gives:
n22=100
- Taking the square root gives:
n2=10
The electron jumps to the quantum level n=10.
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - JEE Main (Archive)
39 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - JEE Advanced (Archive )
67 Videos
- ATOMIC STRUCTUREBOOK - VMC MODULES ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - LEVEL - 2
50 Videos
- AMINESBOOK - VMC MODULES ENGLISHCHAPTER - AMINESEXERCISE - IN CHAPTER EXERCISE H
10 Videos
- CHEMICAL BONDING & CHEMICAL STRUCTURE BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL BONDING & CHEMICAL STRUCTURE EXERCISE - IMPECCABLE
50 Videos
Similar Questions
The speed of the electron in a hydrogen atom in the n = 3 level is
View SolutionAn electron jump from the fourth energy level to the first energy level in hydrogen atom. How many photons of energy are emitted ?
View SolutionThe energy levels of a hypothetical one electron atom are shown in figure
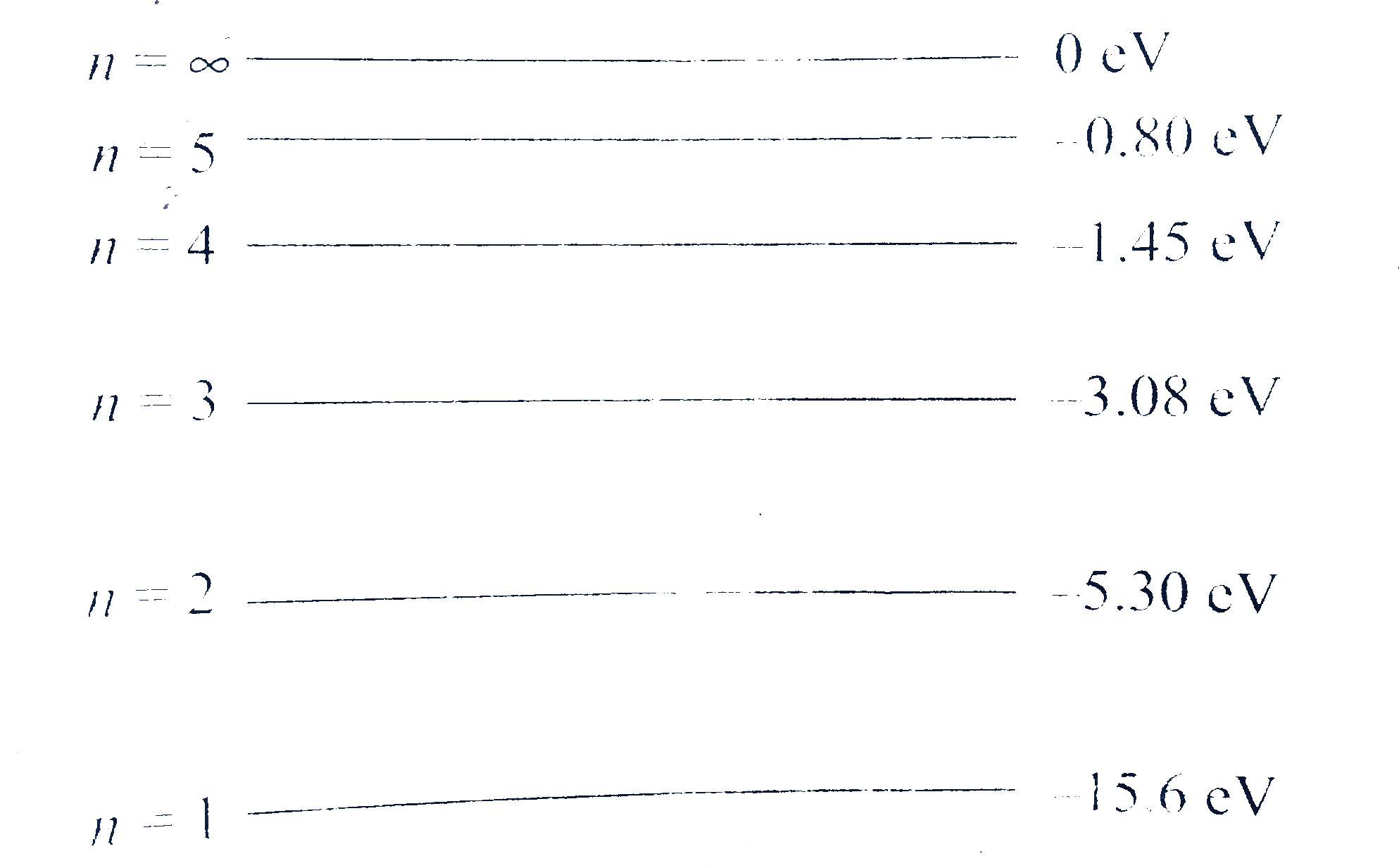
Find the ionization potential of the atom.
View SolutionWhich of the following atoms has the lowest ionization potential ?
View SolutionIf the electron jumps from 7.00 eV energy level to 5.0 eV energy level it
View SolutionAn electron in H atom jumps from the third energy level to the first energy .The charge in the potential energy of the electron is
View SolutionElectrons of energy 12.1 eV are fired at hydrogen atoms in a discharge tube. If the ionization potential of hydrogen is 13.6 eV, then
View SolutionIn hydrogen atom, if the difference in the energy of the electron in n=2 and n=3 orbits is E, the ionization energy of hydrogen atom is
View SolutionThe potential energy of an electron in the fifth orbit of hydrogen atom is
View SolutionAn electron is excited to fourth energy level in an atom. It will
View Solution
