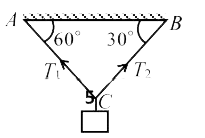
Given that T1=100N then find T2
100√3N
100√3N
50 N
200 N
The correct Answer is:b
T1cos60∘=T2cos30∘
T1(12)=T2√32
10√2sin45∘
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 265videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)12videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)12videos
INTRODUCTION TO VECTORS & FORCES
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)5videos
JEE MAIN - 5
Similar Questions
In a harmonic progression t1,t2,t3,……………., it is given that t5=20andt6=50. If Sn denotes the sum of first n terms of this, then the value of n for which Sn is maximum is
View SolutionA particle is subjected to two simple harmonic motions given by
x1=2.0sin(100πt) and x2=2.0sin(120πt+π/3)
where, x is in cm and t in second. Find the displacement of the particle at
(a) t=0.0125,
(b) t=0.025.View SolutionWhat will be the tension T1andT2 in the given figure?
 View Solution
View SolutionIf nth term (Tn) of the sequece is given by the relation Tn+1=Tn+2n,(nεN) and T1=3, then the value of ∞∑r=11Tr−1 equals
View SolutionLet Tn denotes the nth term of a G.P. with common ratio 2 and (log2(log3(log512T100)))=1. If three sides of a triangle ABC are the values of (T1+T2),T2andT3 then area of the triangle is √2160N, where N is a positive integer. Find the remainder when N is divided by 210.
View SolutionLet Tr denote the rth term of a G.P. for r=1,2,3, If for some positive integers mandn, we have Tm=1/n2 and Tn=1/m2 , then find the value of Tm+n/2.
View SolutionLet Tr denote the rth term of a G.P. for r=1,2,3, If for some positive integers mandn, we have Tm=1/n2 and Tn=1/m2 , then find the value of Tm+n/2.
View SolutionThe first two terms of a sequence are 0 and 1, The nth terms Tn=2Tn−1−Tn−2,n≥3. For example the third terms T3=2T2−T1=2−0=2, The sum of the first 2006 terms of this sequence is :
View SolutionIn Figure, it is given that RT=TS, ∠1=2∠2 and ∠4=2∠3 . Prove that RBT ≅ SAT
View SolutionTwo perfect monoatomic gases at absolute temperature T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases aren1 and n2.
View Solution

