For any two vectors ¯¯¯A and ¯¯¯B if ¯¯¯A.¯¯¯B=∣∣¯¯¯Aׯ¯¯B∣∣, the magnitude of ¯¯¯C=¯¯¯A+¯¯¯B is equal to :
√A2+B2
A+B
√A2+B2+AB√2
√A2+B2+√2×AB
The correct Answer is:d
To solve the problem step by step, we will analyze the given information and apply vector operations.
Step 1: Understand the Given Condition
We are given that for two vectors →A and →B:
→A⋅→B=|→A×→B|
This means that the dot product of the vectors is equal to the magnitude of their cross product.
Step 2: Write the Formulas for Dot Product and Cross Product
The dot product →A⋅→B can be expressed as:
→A⋅→B=|→A||→B|cosθ
where θ is the angle between the two vectors.
The magnitude of the cross product |→A×→B| can be expressed as:
|→A×→B|=|→A||→B|sinθ
Step 3: Set Up the Equation
From the given condition, we can equate the two expressions:
|→A||→B|cosθ=|→A||→B|sinθ
Step 4: Simplify the Equation
Assuming |→A| and |→B| are not zero, we can divide both sides by |→A||→B|:
cosθ=sinθ
Step 5: Solve for θ
The equation cosθ=sinθ implies:
tanθ=1
This means:
θ=45∘
Step 6: Find the Magnitude of →C=→A+→B
The magnitude of the resultant vector →C can be calculated using the formula:
|→C|=|→A+→B|=√|→A|2+|→B|2+2|→A||→B|cosθ
Step 7: Substitute θ into the Formula
Since θ=45∘, we have:
cos45∘=1√2
Substituting this into the equation gives:
|→C|=√|→A|2+|→B|2+2|→A||→B|⋅1√2
Step 8: Simplify the Expression
This simplifies to:
|→C|=√|→A|2+|→B|2+√2|→A||→B|
Final Result
Thus, the magnitude of →C is:
|→C|=√|→A|2+|→B|2+√2|→A||→B|
We are given that for two vectors →A and →B:
→A⋅→B=|→A×→B|
This means that the dot product of the vectors is equal to the magnitude of their cross product.
The dot product →A⋅→B can be expressed as:
→A⋅→B=|→A||→B|cosθ
where θ is the angle between the two vectors.
|→A×→B|=|→A||→B|sinθ
From the given condition, we can equate the two expressions:
|→A||→B|cosθ=|→A||→B|sinθ
Assuming |→A| and |→B| are not zero, we can divide both sides by |→A||→B|:
cosθ=sinθ
The equation cosθ=sinθ implies:
tanθ=1
This means:
θ=45∘
The magnitude of the resultant vector →C can be calculated using the formula:
|→C|=|→A+→B|=√|→A|2+|→B|2+2|→A||→B|cosθ
Since θ=45∘, we have:
cos45∘=1√2
Substituting this into the equation gives:
|→C|=√|→A|2+|→B|2+2|→A||→B|⋅1√2
This simplifies to:
|→C|=√|→A|2+|→B|2+√2|→A||→B|
Thus, the magnitude of →C is:
|→C|=√|→A|2+|→B|2+√2|→A||→B|
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 2
65 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Main ( ARCHIVE ) ( LEVEL-1)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
Knowledge Check
If θ is the angle between any two vectors ¯a and ¯b and ∣∣¯aׯb∣∣=∣∣¯a.¯b∣∣, then value of θ is
Aπ3Bπ2Cπ4Dπ6
If ¯¯¯Aׯ¯¯B=¯¯¯Bׯ¯¯A then the angle between A and B is :
View Solutionthe value of ∮¯¯¯B.¯¯¯dl for the loop L is
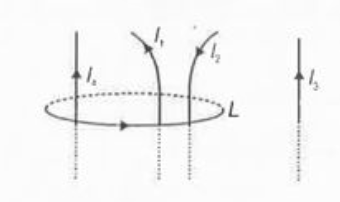
View SolutionIf ¯c=¯aׯband¯b=¯cׯa then
View SolutionShow that vectors ∣∣¯b∣∣¯a+|¯a|¯band∣∣¯b∣∣|¯a−|¯a∣b are orthogonal.
View SolutionIf ˆd is a unit vectors such that ˆd=λ¯bׯc+μ¯cׯa+v¯aׯb then ∣∣(ˆd.¯a)(¯bׯc)+(¯d.¯b)(¯cׯa)+(¯d.¯c)(¯aׯb)∣∣ is equal to
View SolutionFour vectors ¯a,¯b,¯c,and¯d are lying in the same plane. The vectors ¯a and ¯b are equal in magnitude and inclined to each other at an angle of 120∘.¯¯¯C is the resultant of ¯aand¯b. Further ¯a+¯b+¯d=0. If the angle between ¯aand¯dis β and the angle between ¯aand¯cis a, find the correct relation between α and β
View SolutionIF ¯xׯb=¯cׯb and ¯x.¯a =0 then ¯x=
View Solution
