If the road is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid for r=10m ?
0.25
0.18
0.3
0.4
The correct Answer is:A
To solve the problem of determining the minimum friction coefficient required for a scooter traveling at 18 km/hr on a horizontal road with a radius of 10 m, we can follow these steps:
1. Convert the Speed from km/hr to m/s:
The speed of the scooter is given as 18 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
1 km/hr=518 m/s
Therefore,
V=18×518=5 m/s
2. Identify the Given Values:
- Radius of the turn, r=10 m
- Speed of the scooter, V=5 m/s
- Acceleration due to gravity, g=10 m/s2 (approximate value)
3. Apply the Concept of Centripetal Force:
For an object moving in a circular path, the required centripetal force Fc is given by:
Fc=mV2r
where m is the mass of the scooter.
4. Frictional Force:
The frictional force Ff that prevents the scooter from skidding is given by:
Ff=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity.
5. Set Up the Equation:
For the scooter not to skid, the frictional force must be equal to the centripetal force:
mV2r=μmg
6. Cancel the Mass:
Since mass m appears on both sides of the equation, we can cancel it out:
V2r=μg
7. Solve for the Coefficient of Friction μ:
Rearranging the equation gives us:
μ=V2rg
8. Substitute the Known Values:
Now substitute V=5 m/s, r=10 m, and g=10 m/s2:
μ=5210×10=25100=0.25
9. Conclusion:
The minimum coefficient of friction required so that the scooter does not skid is:
μ=0.25
Final Answer:
The minimum friction coefficient required is μ=0.25.
---
The speed of the scooter is given as 18 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
1 km/hr=518 m/s
Therefore,
V=18×518=5 m/s
- Radius of the turn, r=10 m
- Speed of the scooter, V=5 m/s
- Acceleration due to gravity, g=10 m/s2 (approximate value)
For an object moving in a circular path, the required centripetal force Fc is given by:
Fc=mV2r
where m is the mass of the scooter.
The frictional force Ff that prevents the scooter from skidding is given by:
Ff=μmg
where μ is the coefficient of friction and g is the acceleration due to gravity.
For the scooter not to skid, the frictional force must be equal to the centripetal force:
mV2r=μmg
Since mass m appears on both sides of the equation, we can cancel it out:
V2r=μg
Rearranging the equation gives us:
μ=V2rg
Now substitute V=5 m/s, r=10 m, and g=10 m/s2:
μ=5210×10=25100=0.25
The minimum coefficient of friction required so that the scooter does not skid is:
μ=0.25
The minimum friction coefficient required is μ=0.25.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 249videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )16videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)4videos
DYNAMICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE68videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficeint so that a scooter going at 18 km/hr does not skid?
View SolutionIf the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that a scooter going at 18km/h does not skid?
View Solution
Knowledge Check
- Question 1 - Select One
A 4m long ladder weighing 25kg rests with its upper end against a smooth wall and lower end on rough ground.What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
Aa. 0.19Bb. 0.29Cc. 0.39Dd. 0.49
A car goes on a circular horizontal road of radius 100 m. What should be the minimum coefficient of friction between the tyres and the road so that it completes the circle with velocity 10 m/s without slipping ? (Take g=10m/s2)
View SolutionBlock M slides down on frictionless incline as shown. The minimum friction coefficient so that m does not slide with respect to M would be :
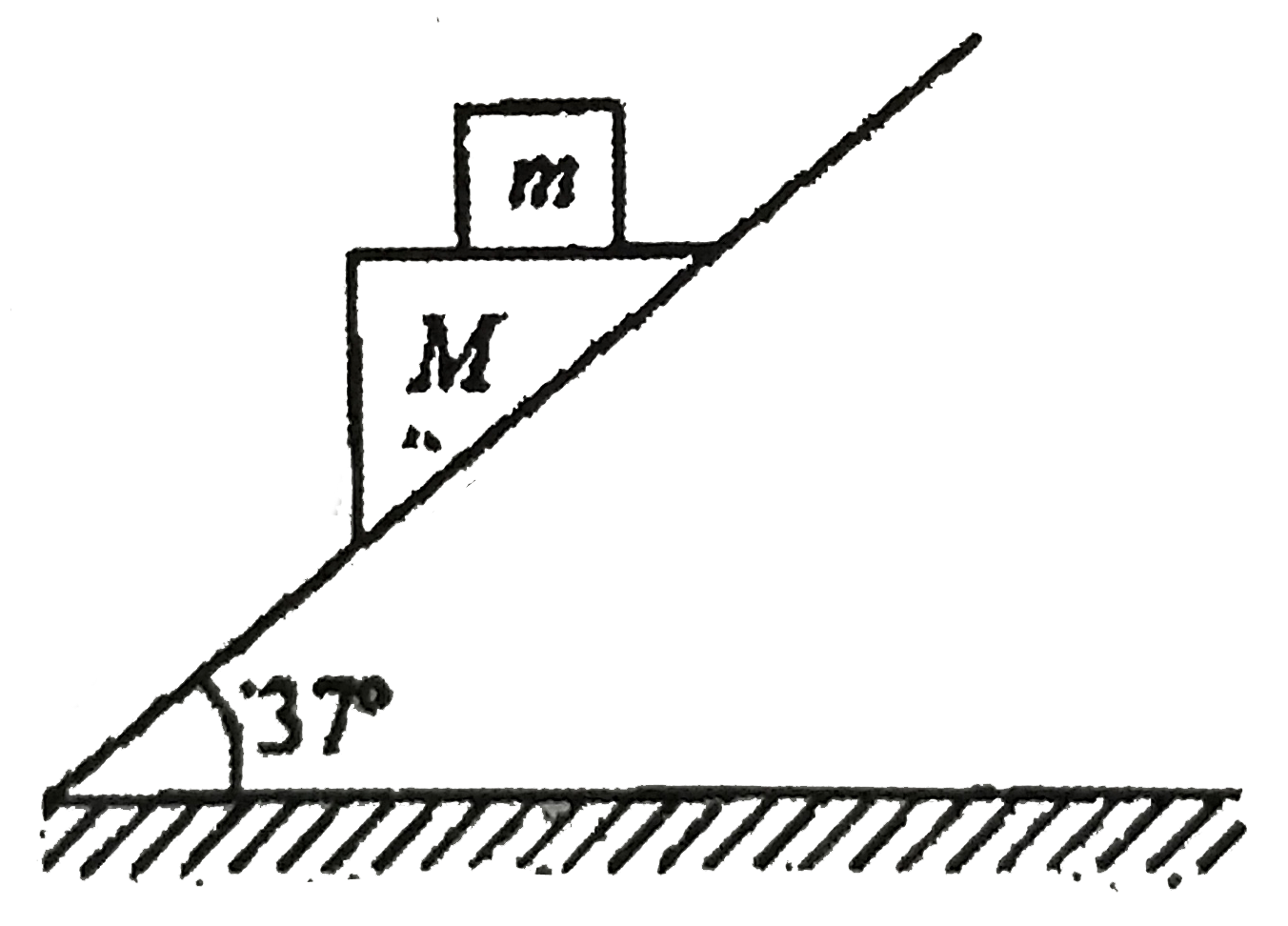 View Solution
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle θ with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View SolutionA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA4m long ladder weighing 25kg rests with its upper and against a smooth wall and lower and on rought ground.What should be the minimum coefficient of friction between the ground and ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
View SolutionIn the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
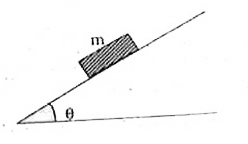 View Solution
View SolutionA bucket tied at the end of a 1.6m long string is whirled in a verticle circle with constant speed. What should be the minimum speed so that the water from the bucket does not spill, when the bucket is at the highest position (Takeg=10m/s2)
View Solution

