Question

A
particle just clears a wall of height b at distance a and strikes the ground
at a distance c from the point of projection. The angle of projection is
(1) $\frac{{\tan }^{-1}b}{ac}$

(2) ${\text{45}}^o$

(3) $\frac{{\tan }^{-1}\left(bc\right)}{a(c-a)}$

(4) $\frac{{\tan }^{-1}\left(bc\right)}{a}$

Options

A. In figure lift is moving along x-axis then value of T may be, zero
B. Lift moving toward right along x-axis with decreasing speed then value of N may be, `gt mg`
C. Lift is moving downward direction with constant velocity then value of T may be, `lt mg`
D. Lift is moving downward direction with constant velocity then value of T may be, = mg

Answer

A::B::C::D

Explanation

`T cos theta = mg implies T = m sqrt((g^(2) + a^(2)))`
`T sin theta = ma `
`implies T gt mg` if a is non-zero and
mg if a is zero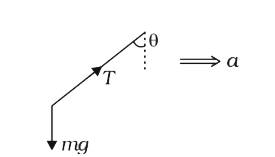
(B) 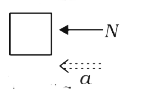`implies` N = ma can be greater less or equal to mg
(c ) 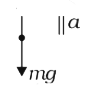`implies` T = mg + ma is greater, less or equal to mg according to as a is positive, negative of zero
(D) 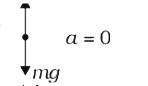`implies ` T = mg