Question

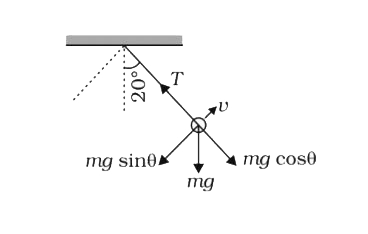
A simple pendulum with a bob of mass m swings with an angular amplitude of ${40}^{\circ }$. When its angular displacement is ${20}^{\circ }$, the tension in the string is greater than $mg{\cos 20}^{\circ }$
true

false

Options

A. (a) true
B. (b) false

Answer

1

Explanation

To determine whether the statement "the tension in the string is greater than mg cos 20°" is true or false when the angular displacement of a simple pendulum is 20°, we can analyze the forces acting on the pendulum bob.

1. Understanding the Forces Acting on the Bob:
- When the pendulum swings, the forces acting on the bob (mass m) are:
- The gravitational force (mg) acting vertically downward.
- The tension (T) in the string acting along the string towards the pivot.

2. Resolving the Gravitational Force:
- The gravitational force can be resolved into two components:
- A component along the direction of the tension: \( mg \cos \theta \)
- A component perpendicular to the tension (which contributes to the motion): \( mg \sin \theta \)
- Here, \( \theta \) is the angle of displacement from the vertical, which is 20° in this case.

3. Applying Newton's Second Law:
- For the pendulum bob, the net force acting towards the center of the circular path (which is the tension minus the component of weight acting along the string) must equal the centripetal force required for circular motion.
- The equation can be expressed as:
\( T - mg \cos(20°) = \frac{mv^2}{L} \)
- Where \( L \) is the length of the pendulum and \( v \) is the velocity of the bob at that position.

4. Rearranging the Equation:
- Rearranging gives us:
\( T = mg \cos(20°) + \frac{mv^2}{L} \)
- Since \( \frac{mv^2}{L} \) is a positive quantity (the bob is in motion), it follows that:
\( T > mg \cos(20°) \)

5. Conclusion:
- Therefore, when the angular displacement is 20°, the tension in the string is indeed greater than \( mg \cos(20°) \).
- Thus, the statement is true.

Final Answer:
The statement is true.