Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
1.67×10−9(ˆi−ˆj)N
3.34×10−10(ˆi−ˆj)N
1.67×10−9(ˆi+ˆj)N
3.34×10−10(ˆi+ˆj)N
The correct Answer is:C
To find the net gravitational force on the mass at the origin (0,0) due to the other two masses located at (0,0.2m) and (0.2m,0), we can follow these steps:
Step 1: Identify the masses and their positions
We have three identical point masses, each of mass m=1kg:
- Mass A at (0, 0) (the origin)
- Mass B at (0, 0.2m)
- Mass C at (0.2m, 0)
Step 2: Calculate the gravitational force exerted on mass A by mass B
The gravitational force FAB between two point masses is given by the formula:
F=G⋅m1⋅m2r2
Where:
- G is the gravitational constant (6.67×10−11N m2/kg2)
- m1=m2=1kg
- r is the distance between the two masses. The distance between A and B is 0.2m.
Calculating FAB:
FAB=G⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
The direction of this force is downward (in the negative y-direction), so we can express it as:
FAB=−1.6675×10−9^j
Step 3: Calculate the gravitational force exerted on mass A by mass C
Now, we calculate the gravitational force FAC between mass A and mass C. The distance between A and C is also 0.2m.
Calculating FAC:
FAC=G⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
The direction of this force is to the right (in the positive x-direction), so we can express it as:
FAC=1.6675×10−9^i
Step 4: Calculate the net gravitational force on mass A
The net gravitational force Fnet on mass A is the vector sum of FAB and FAC:
Fnet=FAB+FAC=(−1.6675×10−9^j)+(1.6675×10−9^i)
Thus,
Fnet=1.6675×10−9^i−1.6675×10−9^j
Step 5: Express the final answer
The net gravitational force on the mass at the origin can be expressed as:
Fnet=1.6675×10−9^i−1.6675×10−9^jN
We have three identical point masses, each of mass m=1kg:
- Mass A at (0, 0) (the origin)
- Mass B at (0, 0.2m)
- Mass C at (0.2m, 0)
The gravitational force FAB between two point masses is given by the formula:
F=G⋅m1⋅m2r2
Where:
- G is the gravitational constant (6.67×10−11N m2/kg2)
- m1=m2=1kg
- r is the distance between the two masses. The distance between A and B is 0.2m.
FAB=G⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
The direction of this force is downward (in the negative y-direction), so we can express it as:
FAB=−1.6675×10−9^j
Now, we calculate the gravitational force FAC between mass A and mass C. The distance between A and C is also 0.2m.
FAC=G⋅1⋅1(0.2)2=6.67×10−110.04=1.6675×10−9N
The direction of this force is to the right (in the positive x-direction), so we can express it as:
FAC=1.6675×10−9^i
The net gravitational force Fnet on mass A is the vector sum of FAB and FAC:
Fnet=FAB+FAC=(−1.6675×10−9^j)+(1.6675×10−9^i)
Thus,
Fnet=1.6675×10−9^i−1.6675×10−9^j
The net gravitational force on the mass at the origin can be expressed as:
Fnet=1.6675×10−9^i−1.6675×10−9^jN
Topper's Solved these Questions
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-2
30 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)
43 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - LEVEL -0 Long Answer Type
3 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
Similar Questions
A large number of identical point masses m are placed along x - axis ,at x = 0,1,2,4,……… The magnitude of gravitational force on mass at origin ( x =0) , will be
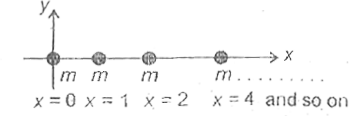
View SolutionTwo bodies of masses 10 kg and 20 kg are located in x-y plane at (0, 1) and (1, 0). The position of their centre of mass is
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View SolutionTwo bodies of masses 1 kg and 3 kg are lying in xy plane at (0, 0) and (2, -1) respectively. What are the coordinates of the centre of mass ?
View SolutionThe gravitational field in a region is given by →E=(5Nkg−1)→i+(12Nkg−1)→j.. a. find the magnitude of the gravitational force acting on a particle of mass 2 kg placed at the origin b. Find the potential at the points (12m,0) and (0,5m) if the potential at the origin is taken to be zero. c. Find the change in gravitational potential energy if a particle of mass 2 kg is taken from the origin to the point (12m,5m). d. Find the change in potential energy if the particle is taken from (12m,0) to (0,5m).
View SolutionTwo small particles P and Q each of mass m are fixed along x-axis at points (a,0) and (-a,0). A third particle R is kept at origin. Then
View SolutionThe gravitational force on a body of mass 1.5 kg situated at a point is 45 M . The gravitational field intensity at that point is .
View Solution
