Two satellites of same mass are orbiting round the earth at heights of r1 and r2 from the centre of earth. Their kinetic energies are in the ratio of :
r2r1
r1r2
r1(r1+r2)
r2(r1+r2)
The correct Answer is:A
To solve the problem of finding the ratio of the kinetic energies of two satellites orbiting the Earth at different heights, we can follow these steps:
1. Understanding the Forces:
Each satellite experiences a gravitational force that acts as the centripetal force necessary for circular motion. The gravitational force Fg acting on a satellite of mass m at a distance r from the center of the Earth (where the mass of the Earth is M) is given by:
Fg=GMmr2
where G is the gravitational constant.
2. Centripetal Force:
The centripetal force required to keep the satellite in circular motion is given by:
Fc=mv2r
where v is the orbital speed of the satellite.
3. Equating Forces:
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal:
GMmr2=mv2r
4. Canceling Mass:
Since the mass m of the satellite is the same for both satellites, we can cancel it from both sides:
GMr2=v2r
5. Rearranging for Velocity:
Rearranging the equation gives us:
v2=GMr
6. Kinetic Energy:
The kinetic energy K of a satellite is given by:
K=12mv2
Substituting v2 from the previous step, we get:
K=12m(GMr)=GMm2r
7. Finding the Ratio of Kinetic Energies:
Let K1 be the kinetic energy of the first satellite at distance r1 and K2 be the kinetic energy of the second satellite at distance r2:
K1=GMm2r1andK2=GMm2r2
To find the ratio of the kinetic energies:
K1K2=GMm2r1GMm2r2=r2r1
8. Conclusion:
The ratio of the kinetic energies of the two satellites is:
K1K2=r2r1
Final Answer:
The kinetic energies of the two satellites are in the ratio K1K2=r2r1.
---
Each satellite experiences a gravitational force that acts as the centripetal force necessary for circular motion. The gravitational force Fg acting on a satellite of mass m at a distance r from the center of the Earth (where the mass of the Earth is M) is given by:
Fg=GMmr2
where G is the gravitational constant.
The centripetal force required to keep the satellite in circular motion is given by:
Fc=mv2r
where v is the orbital speed of the satellite.
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal:
GMmr2=mv2r
Since the mass m of the satellite is the same for both satellites, we can cancel it from both sides:
GMr2=v2r
Rearranging the equation gives us:
v2=GMr
The kinetic energy K of a satellite is given by:
K=12mv2
Substituting v2 from the previous step, we get:
K=12m(GMr)=GMm2r
Let K1 be the kinetic energy of the first satellite at distance r1 and K2 be the kinetic energy of the second satellite at distance r2:
K1=GMm2r1andK2=GMm2r2
To find the ratio of the kinetic energies:
K1K2=GMm2r1GMm2r2=r2r1
The ratio of the kinetic energies of the two satellites is:
K1K2=r2r1
The kinetic energies of the two satellites are in the ratio K1K2=r2r1.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level-230videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Main (Archive)43videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - LEVEL -0 Long Answer Type3videos
GRAVITATION
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)12videos
INTRODUCTION TO VECTORS & FORCES
Similar Questions
Knowledge Check
- Question 1 - Select One
A satellite of a mass m orbits the earth at a height h above the surface of the earth. How much energy must be expended to rocket the satellite out of earth's gravitational influence? (where ME and RE be mass and radius of the earth respectively)
AGMEm4(RE+h)BGMEm2(RE+h)CGMEm(RE+h)D2GMEm(RE+h)
Two small satellites are moving in circular orbits around the earth at a distance R and R+ΔR from the centre of the earth. If their time period of rotation are T and T+ΔT respectively, then
View SolutionTwo satellites A and B of the same mass are orbiting the earth at altitudes R and 3R respectively, where R is the radius of the earth. Taking their orbit to be circular obtain the ratios of their kinetic and potential energies.
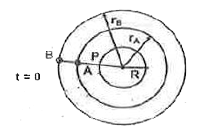
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
 View Solution
View SolutionTwo satellites S1 and S2 revolve around the earth at distances 3R and 6R from the centre of the earth. Find the ratio of their (a) linear speeds and (b) angular speeds.
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionIf the kinetic energy of a satellite orbiting around the earth is doubled then
View Solution

