Two carnot engines A and B are operated in series. The first one A receives heat at 900K and rejects it to a reservoir at TK. The second engine B receives the heat rejected by the first engine and rejects it to a heat reservoir at 400K. Calculate the value of T, when the efficiency ot two engines is the same.
To solve the problem of finding the temperature T at which the efficiencies of two Carnot engines A and B are the same, we can follow these steps:
Step 1: Understand the Carnot Engine Efficiency Formula
The efficiency η of a Carnot engine is given by the formula:
η=1−TcoldThot
where Thot is the temperature at which the engine absorbs heat and Tcold is the temperature at which it rejects heat.
Step 2: Write the Efficiency for Engine A
For engine A:
- Thot=900K
- Tcold=TK
The efficiency of engine A (ηA) can be expressed as:
ηA=1−T900
Step 3: Write the Efficiency for Engine B
For engine B:
- Thot=TK (the heat rejected by engine A is absorbed by engine B)
- Tcold=400K
The efficiency of engine B (ηB) can be expressed as:
ηB=1−400T
Step 4: Set the Efficiencies Equal
According to the problem, the efficiencies of both engines are the same:
ηA=ηB
Substituting the expressions for ηA and ηB:
1−T900=1−400T
Step 5: Simplify the Equation
We can simplify the equation by eliminating the 1s on both sides:
−T900=−400T
Multiplying through by -1 gives:
T900=400T
Step 6: Cross Multiply
Cross multiplying gives:
T2=400×900
Step 7: Calculate T2
Calculating the right side:
T2=360000
Step 8: Solve for T
Taking the square root of both sides:
T=√360000=600K
Final Answer
Thus, the value of T is:
600K
The efficiency η of a Carnot engine is given by the formula:
η=1−TcoldThot
where Thot is the temperature at which the engine absorbs heat and Tcold is the temperature at which it rejects heat.
For engine A:
- Thot=900K
- Tcold=TK
ηA=1−T900
For engine B:
- Thot=TK (the heat rejected by engine A is absorbed by engine B)
- Tcold=400K
ηB=1−400T
According to the problem, the efficiencies of both engines are the same:
ηA=ηB
Substituting the expressions for ηA and ηB:
1−T900=1−400T
We can simplify the equation by eliminating the 1s on both sides:
−T900=−400T
Multiplying through by -1 gives:
T900=400T
Cross multiplying gives:
T2=400×900
Calculating the right side:
T2=360000
Taking the square root of both sides:
T=√360000=600K
Thus, the value of T is:
600K
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 1
75 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 2
40 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – I
10 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
Two Camot engines A and B are operated in series. The first one, A , receives heat at T1(=600K) and rejects to a reservoir at temperature T2. The second engine B receives heat rejected by the first engine and, in turn, rejects to a heat reservoir at T3(=400K). Calculate the temperature T2 if the work outputs of the two engines are equal :
View SolutionTwo carnot engines A and B are operated in series .Engine A receives heat from a reservoier at 600 K and rejectrs heat to a reservoir at temperatures T. Engine B receives heat rejected by engine A and in turn rejects it to a reservoir at 100 K .If the efficiencies of the two engines A and B are represented by ηAandηB repectively then what is the value of ηBηA?
View Solution
Knowledge Check
A heat engine has an efficiency η.Temperatures of source and sink are each decreased by 100 K. The efficiency of the engine
AIncreasesBDecreasesCRemains constantDBecomes 1
Two Carnot engines A and B are operated in series. The engine A receives heat from the source at temperature T1 and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T2. For what value of T the efficiencies of the two engines are equal?
View SolutionTwo heat engines are operating in such a way that the heat rejected by the first engine is used as the heat input of the second. If both the engines are 40% efficient, then the overall efficiency of the system is
View SolutionA carnot engine operates between two reservoirs of temperature 900K and 300K. The engine performs 1200 J of work per cycle. The heat energy delivered by the engine to the low temperature reservoir in a cycle is:
View SolutionA carnot engine operates between two reservoirs of temperature 900K and 300K. The engine performs 1200 J of work per cycle. The heat energy delivered by the engine to the low temperature reservoir in a cycle is:
View SolutionCarnot engine takes one thousand kilo calories of heat from a reservoir at 827∘C and exhausts it to a sink at 27∘C. How, much work does it perform? What is the efficiency of the engine?
View SolutionWhen steady state is reached, switch S is opened. Then the amount of heat rejected by the resistor is 800K Joule. Then find the value of K.
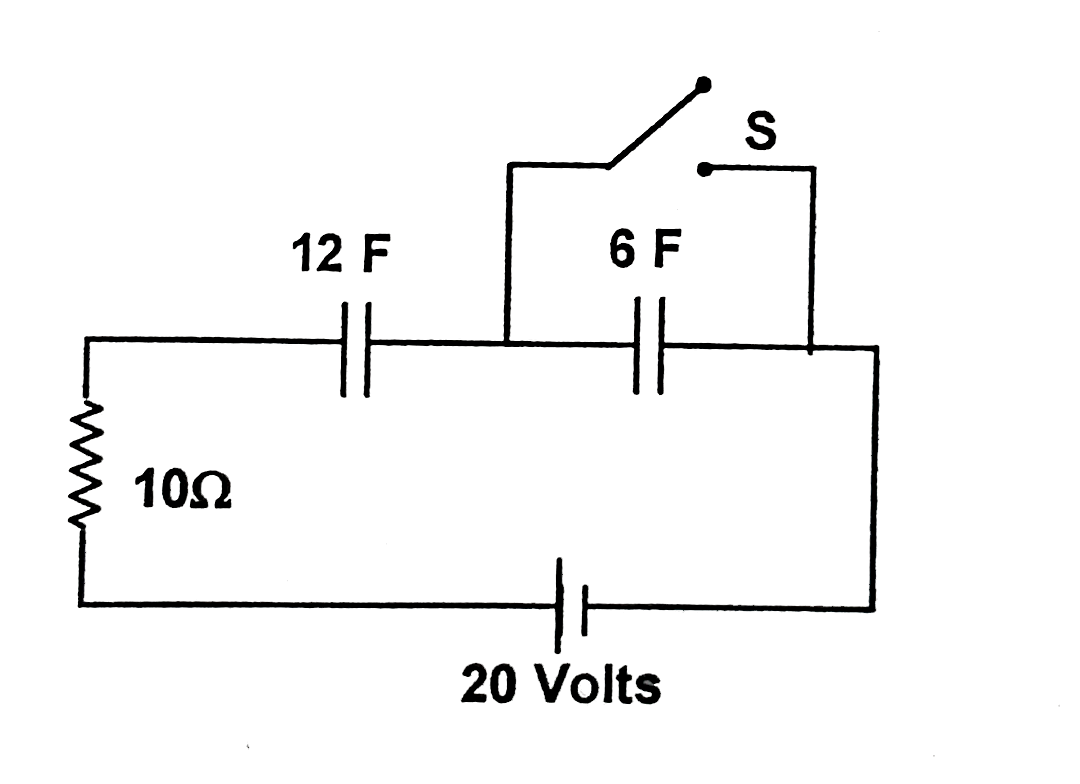
View SolutionA carnot engine is operated between two reserviors at temperatures of 500 K and 400 K. The engine receives 840 Joules of heat from the source in each cycle. Calculate (a) the amount of heat rejected to sink in each cycle (b) the efficiency of the engine, and (c) the work done in each cycle.
View Solution