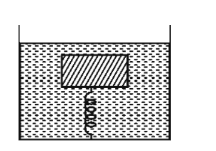
A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touched the free end of a massless spring of force constant k fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
a(a2ρg+K)
a(aρg+2K)
a(aρg2+2K)
a(a2ρg+K2)
The correct Answer is:D
(##VMCPHYXIWORBOK02_C08E02017_S01.png width=80%><br> rArr Densityofblock=12(densityofwater)<br>W=Extraupthust+Spr∈gforce<br> rArr a xx a xx (a)/(2) 2 rho xx g + K ((a )/(2)) rArr a (a ^ 2 rho g + (K)/(2))
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )31videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )15videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
A cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cubical block 'A' of mass m0(=a3ρ=3kg) of edge 'a' and density ρ floats in a liquid of density 3ρ. The lower surface of the cube just touches the free end of massless spring of spring of spring constant k(=a2ρg) fixed at the bottom of the vessel. Another block 'B' of mass 'm' is lept over block 'A', so that is completely immersed in liquid without wetting the block 'B'. Then find the value of m in kg.
View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View SolutionA cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View SolutionA cubic block of side a is connected with two similar vertical springs as shown. Initially, bottom surface of the block of density σ touches the surface of the fluid of density 2σ while floating. A weight is placed on the block so that it is immersed half in the fluid, find the weight.
 View Solution
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is
 View Solution
View SolutionA wooden block of mass 8 kg is tied to a string attached to the bottome of the tank. In the equilibrium the block is completely immersed in water. If relative density of wood is 0.8 and g=10ms−2, the tension T, in the string is
View SolutionA wooden block of mass 0.5 kg and density 800 kgm−3 is fastened to the free end of a vertical spring of spring constant 50 Nm−1 fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compression) of the spring in equilibrium and b. the time period of vertical oscillations of the block when it is slightly depressed and released.
View SolutionA cube of wood of mass 0.5 kg and density 800kgm−3 is fastened to the free end of a vertical spring of spring constant k=50Nm−1 fixed at the bottom. Now, the entire system is completely submerged in water. The elongation or compression of the spring in equilibrium is β2cm. Find the value of β . (Given g=10ms−2 )
 View Solution
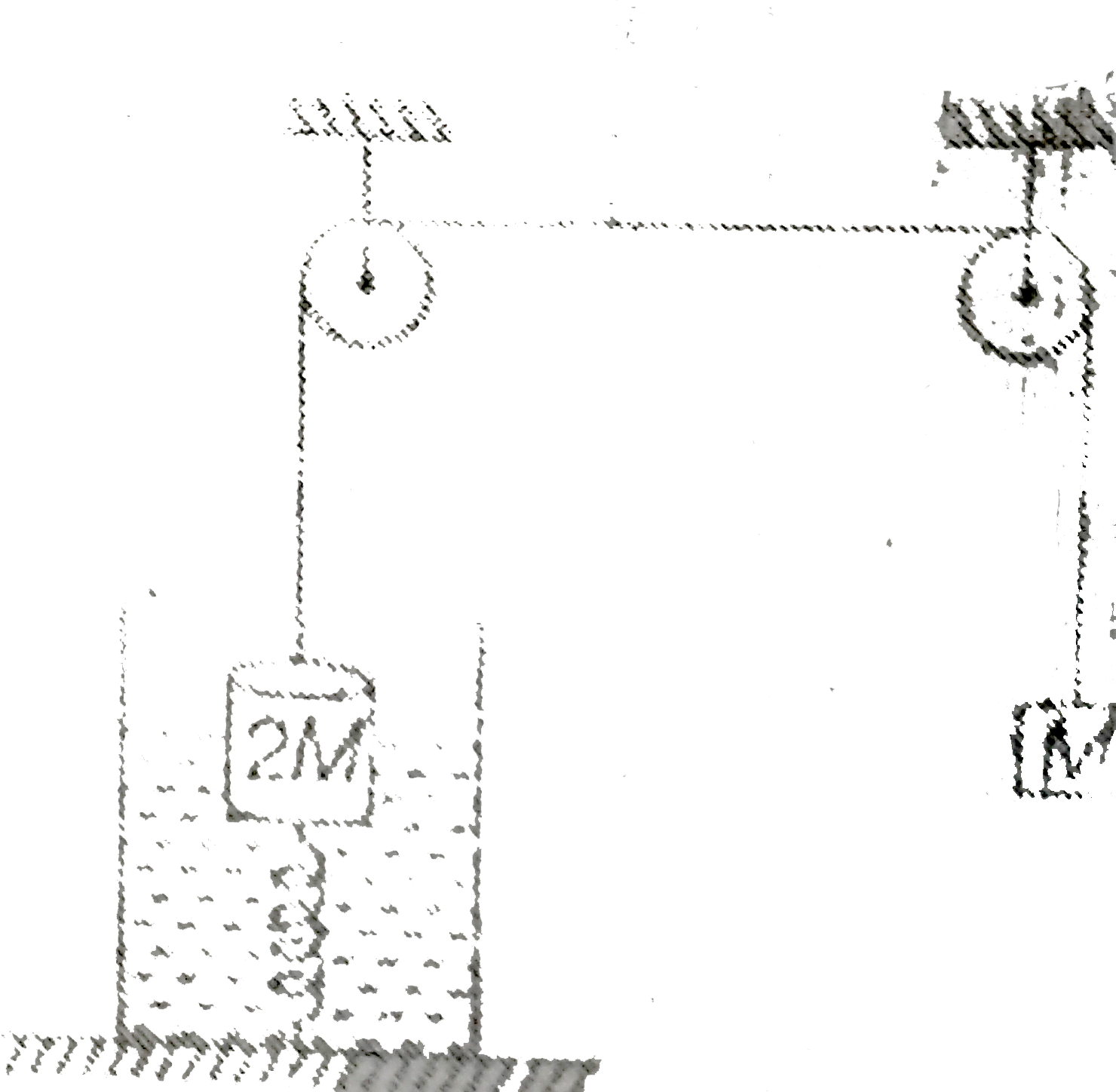
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
 View Solution
View Solution

