A liquid whose coefficient of viscosity is η flows on a horizontal surface. Let dx represent the vertical distance between two layers of liquid and dv represent the difference in the velocities of the two layers. Then the quantity η(dv/dx) has the same dimensions as:
Acceleration
Force
Momentum
Pressure
The correct Answer is:D
To solve the problem, we need to analyze the quantity η(dvdx) and determine its dimensions.
1. Understanding the Terms:
- η is the coefficient of viscosity, which is a measure of a fluid's resistance to flow.
- dv represents the difference in velocities between two layers of the liquid.
- dx represents the vertical distance between those two layers.
2. Velocity Gradient:
- The term dvdx represents the velocity gradient, which is the change in velocity per unit distance.
3. Dimensions of Velocity:
- Velocity v has dimensions of (LT−1), where L is length and T is time.
4. Dimensions of Distance:
- The distance dx has dimensions of (L).
5. Calculating Dimensions of Velocity Gradient:
- The dimensions of the velocity gradient dvdx can be calculated as follows:
(dvdx)=(LT−1)(L)=(T−1)
6. Dimensions of Coefficient of Viscosity:
- The coefficient of viscosity η is defined as the ratio of shear stress to the velocity gradient. The dimensions of shear stress are:
Shear Stress=ForceArea=(MLT−2)(L2)=(ML−1T−2)
- Therefore, the dimensions of viscosity η can be expressed as:
(η)=(Shear Stress)(Velocity Gradient)=(ML−1T−2)(T−1)=(ML−1T−1)
7. Combining the Dimensions:
- Now, we can find the dimensions of the quantity η(dvdx):
(η(dvdx))=(ML−1T−1)⋅(T−1)=(ML−1T−2)
8. Identifying the Result:
- The dimensions (ML−1T−2) correspond to pressure, as pressure is defined as force per unit area.
Conclusion:
Thus, the quantity η(dvdx) has the same dimensions as pressure.
Final Answer:
The quantity η(dvdx) has the same dimensions as pressure.
---
- η is the coefficient of viscosity, which is a measure of a fluid's resistance to flow.
- dv represents the difference in velocities between two layers of the liquid.
- dx represents the vertical distance between those two layers.
- The term dvdx represents the velocity gradient, which is the change in velocity per unit distance.
- Velocity v has dimensions of (LT−1), where L is length and T is time.
- The distance dx has dimensions of (L).
- The dimensions of the velocity gradient dvdx can be calculated as follows:
(dvdx)=(LT−1)(L)=(T−1)
- The coefficient of viscosity η is defined as the ratio of shear stress to the velocity gradient. The dimensions of shear stress are:
Shear Stress=ForceArea=(MLT−2)(L2)=(ML−1T−2)
- Therefore, the dimensions of viscosity η can be expressed as:
(η)=(Shear Stress)(Velocity Gradient)=(ML−1T−2)(T−1)=(ML−1T−1)
- Now, we can find the dimensions of the quantity η(dvdx):
(η(dvdx))=(ML−1T−1)⋅(T−1)=(ML−1T−2)
- The dimensions (ML−1T−2) correspond to pressure, as pressure is defined as force per unit area.
Thus, the quantity η(dvdx) has the same dimensions as pressure.
The quantity η(dvdx) has the same dimensions as pressure.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )31videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )15videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
A liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
View SolutionIf η represents the coefficient of viscosity and T the surface tension. Then the dimensions of T/η are same as that of
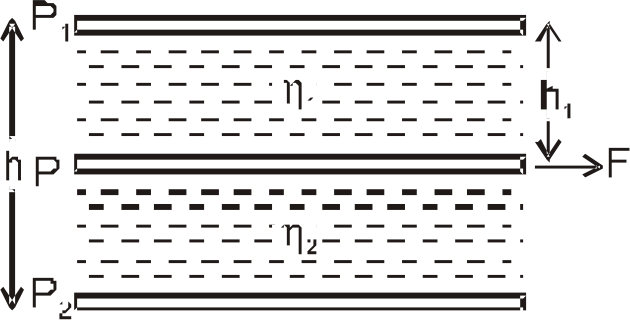
View SolutionA thin horizontal movable plate P is separated from two fixed horizontal plates P1 and P2 by two highly viscous liquids of coefficient of viscosity η1 and η2 as shown, where η2=4η1. Area of contact of movable plate with each fluid is same. If the distance between two fixed plates is h, then the distance h1 of movable plate from upper fixed plate such that the movable plate can be moved with a constant velocity by applying a minimum constant horizontal force F on movable plate is (assume velocity gradient to be uniform in each liquid).
 View Solution
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
 View Solution
View SolutionThe viscous force acting between two layers of a liquid is given by FA=ηdvdz. This F/A may be called
View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , eta = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2) , where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The velocity of flow of liquid at r = R/2 isView SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical vloume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal

This is called Poisecuille's equation .
The volume of the liquid flowing per sec across the cross - section of the tube is .View SolutionWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48ηL
This is called Poisecuille's equation .

The viscous force on the cylindrical volume of the liquid varies asView SolutionThe coefficient of viscosity (η) of a fluid moving steadily between two surface is given by the formula (f)=ηAdV/dx where f is the frictional force on the flluid, A is the area in the fluid, and dN/dx is velocity gradient inside the fluid at that area. The SI unit of viscosity is given as :
View SolutionWhen a liquid flows in a tube, there is relative motion between adjacent layers of the liquid. This force is called the viscous force which tends to oppose the relative motion between the layers of the liquid. Newton was the first person to study the factors that govern the viscous force in a liquid. According to Newton’s law of viscous flow, the magnitude of the viscous force on a certain layer of a liquid is given by
F=−ηAdvdx
where A is the area of the layer dvdx is the velocity gradient at the layer and η is the coefficient of viscosity of the liquid.
The dimensional formula for the coefficient of viscosity is :View Solution

