A liquid at 30°C is poured verly slowly into a Calorimeter that is at temperature of 110°C. The boiling temperature of the liquid is 80°C. It is found that the first 5 gm of the liquid completely evaporates. After pouring another 80 gm of the liquid the equilibrium temperature is found to be 50°C. The ratio of the Latent heat of the liquid to its specific heat will be ____C°.
[Neglect the heat exchange with surrounding.]
The correct Answer is:270.00
To solve the problem, we will analyze the heat exchanges that occur when the liquid is poured into the calorimeter.
1. Understanding the Problem:
- We have a liquid at 30°C being poured into a calorimeter at 110°C.
- The boiling point of the liquid is 80°C.
- The first 5 grams of the liquid completely evaporate.
- After pouring an additional 80 grams of the liquid, the equilibrium temperature is found to be 50°C.
2. Heat Required for Evaporation:
- The first 5 grams of the liquid must be heated from 30°C to 80°C (its boiling point) and then evaporated.
- The heat required to raise the temperature of the liquid from 30°C to 80°C:
Q1=m⋅c⋅ΔT=5g⋅c⋅(80−30)=5c⋅50=250c(calories)
- The heat required for the evaporation of the liquid (latent heat):
Q2=m⋅Lv=5⋅Lv(calories)
3. Heat Lost by Calorimeter:
- The calorimeter cools down from 110°C to 80°C while supplying heat to the 5 grams of liquid.
- The heat lost by the calorimeter:
Q3=H⋅ΔT=H⋅(110−80)=30H
- By the conservation of energy, the heat gained by the liquid equals the heat lost by the calorimeter:
Q1+Q2=Q3
- Substituting the values:
250c+5Lv=30H(Equation 1)
4. Heat Exchange with Additional 80 grams of Liquid:
- The additional 80 grams of liquid is heated from 30°C to 50°C.
- The heat gained by the 80 grams of liquid:
Q4=80⋅c⋅(50−30)=80c⋅20=1600c(calories)
- The calorimeter cools from 80°C to 50°C:
Q5=H⋅(80−50)=30H
- Again, by conservation of energy:
Q4=Q5
- Substituting the values:
1600c=30H(Equation 2)
5. Solving the Equations:
- From Equation 2, we can express H:
H=1600c30=160c3
- Substitute H back into Equation 1:
250c+5Lv=30(160c3)
250c+5Lv=1600c
5Lv=1600c−250c
5Lv=1350c
Lv=1350c5=270c
6. Finding the Ratio of Latent Heat to Specific Heat:
- The ratio of the latent heat Lv to the specific heat c:
Lvc=270cc=270
Final Answer:
The ratio of the latent heat of the liquid to its specific heat is 270°C.
- We have a liquid at 30°C being poured into a calorimeter at 110°C.
- The boiling point of the liquid is 80°C.
- The first 5 grams of the liquid completely evaporate.
- After pouring an additional 80 grams of the liquid, the equilibrium temperature is found to be 50°C.
- The first 5 grams of the liquid must be heated from 30°C to 80°C (its boiling point) and then evaporated.
- The heat required to raise the temperature of the liquid from 30°C to 80°C:
Q1=m⋅c⋅ΔT=5g⋅c⋅(80−30)=5c⋅50=250c(calories)
- The heat required for the evaporation of the liquid (latent heat):
Q2=m⋅Lv=5⋅Lv(calories)
- The calorimeter cools down from 110°C to 80°C while supplying heat to the 5 grams of liquid.
- The heat lost by the calorimeter:
Q3=H⋅ΔT=H⋅(110−80)=30H
- By the conservation of energy, the heat gained by the liquid equals the heat lost by the calorimeter:
Q1+Q2=Q3
- Substituting the values:
250c+5Lv=30H(Equation 1)
- The additional 80 grams of liquid is heated from 30°C to 50°C.
- The heat gained by the 80 grams of liquid:
Q4=80⋅c⋅(50−30)=80c⋅20=1600c(calories)
- The calorimeter cools from 80°C to 50°C:
Q5=H⋅(80−50)=30H
- Again, by conservation of energy:
Q4=Q5
- Substituting the values:
1600c=30H(Equation 2)
- From Equation 2, we can express H:
H=1600c30=160c3
- Substitute H back into Equation 1:
250c+5Lv=30(160c3)
250c+5Lv=1600c
5Lv=1600c−250c
5Lv=1350c
Lv=1350c5=270c
- The ratio of the latent heat Lv to the specific heat c:
Lvc=270cc=270
The ratio of the latent heat of the liquid to its specific heat is 270°C.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (NUMBERICAL VALUE TYPE)
7 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (FILL IN THE BLANKS TYPE )
11 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2
29 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
In a solid ⇔ liquid equilibrium , temperature remains constant.
View SolutionHigher the initial temperature of the liquid, more is the rate of evaporation of liquid.
View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View SolutionTwo liquids A and B are at 30∘C and 20∘C, respectively When they are mixied in equal masses, the temperature of the mixture is found to be 26∘C. The ratio of their specific heat is
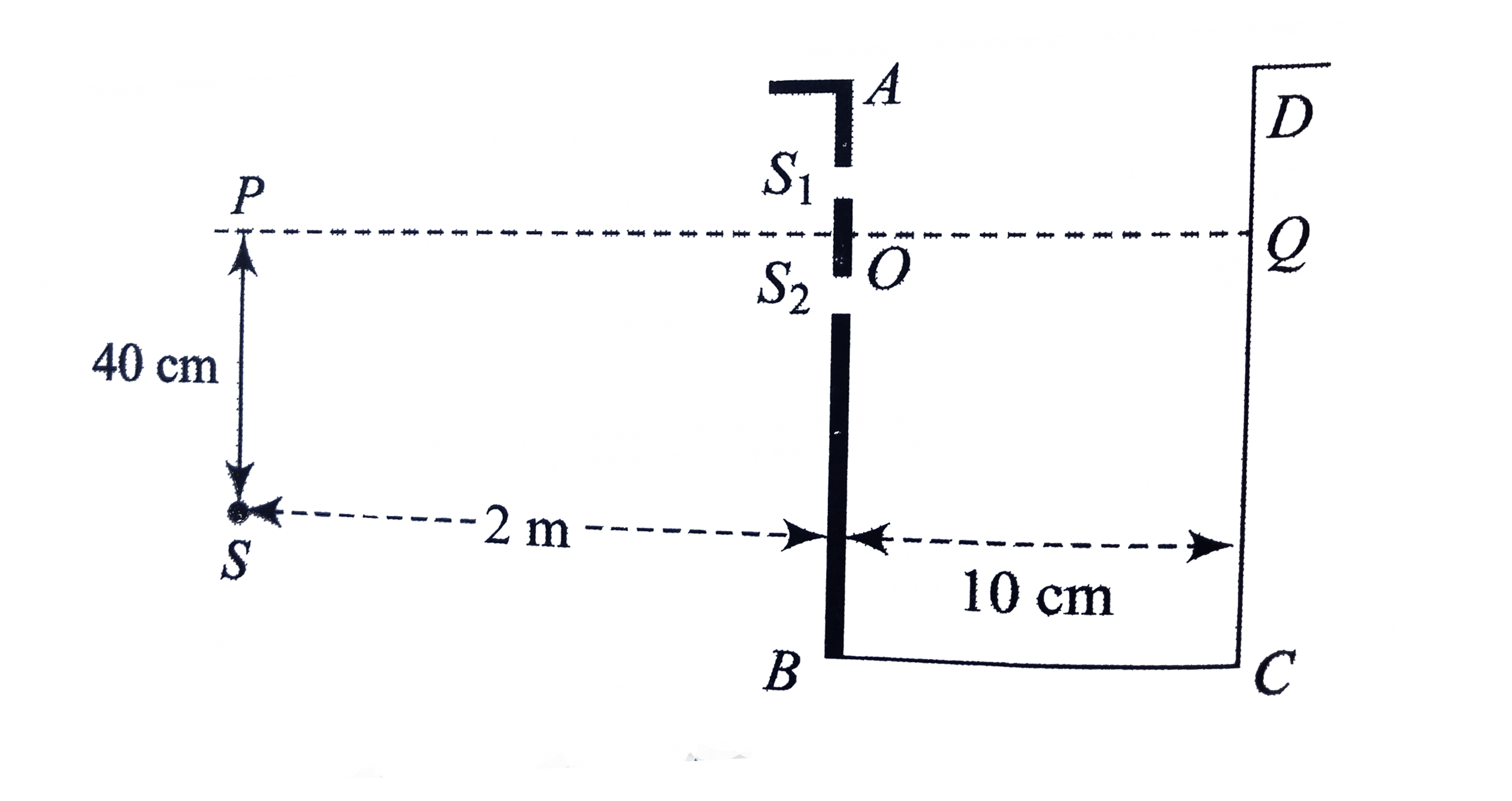
View SolutionA vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line peropendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m form the vessel to illuminate the slits as shown in figure .Calculate the position of the central bright fringe on the other wall CD with respect to line OQ. Now , a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid to the liquid.
View SolutionSteam is passed into 54gm of water at 30∘C till the temperature of mixture becomes 90∘C. If the latent heat of steam is 536cal/gm, the mass of the mixture will be
View SolutionTwo liquid A and B are at 32∘C and 24∘C. When mixed in equal masses the temperature of the mixture is found to be 28∘C. Their specific heats are in the ratio of
View SolutionTwo liquids are at temperatures 20∘Cand40∘C. When same mass of both of them is mixed, the temperature of the mixture is 32∘C. What is the ratio of their specific heats?
View SolutionWhat happens if a liquid is heated to the critical temperature of its vapour?
View SolutionTwo liquids at temperature 60∘C and 20∘C respectively have masses in the ratio 3:4 their specific heat in the ratio 4:5. If the two liquids are mixed, the resultant temperature is.
View Solution
