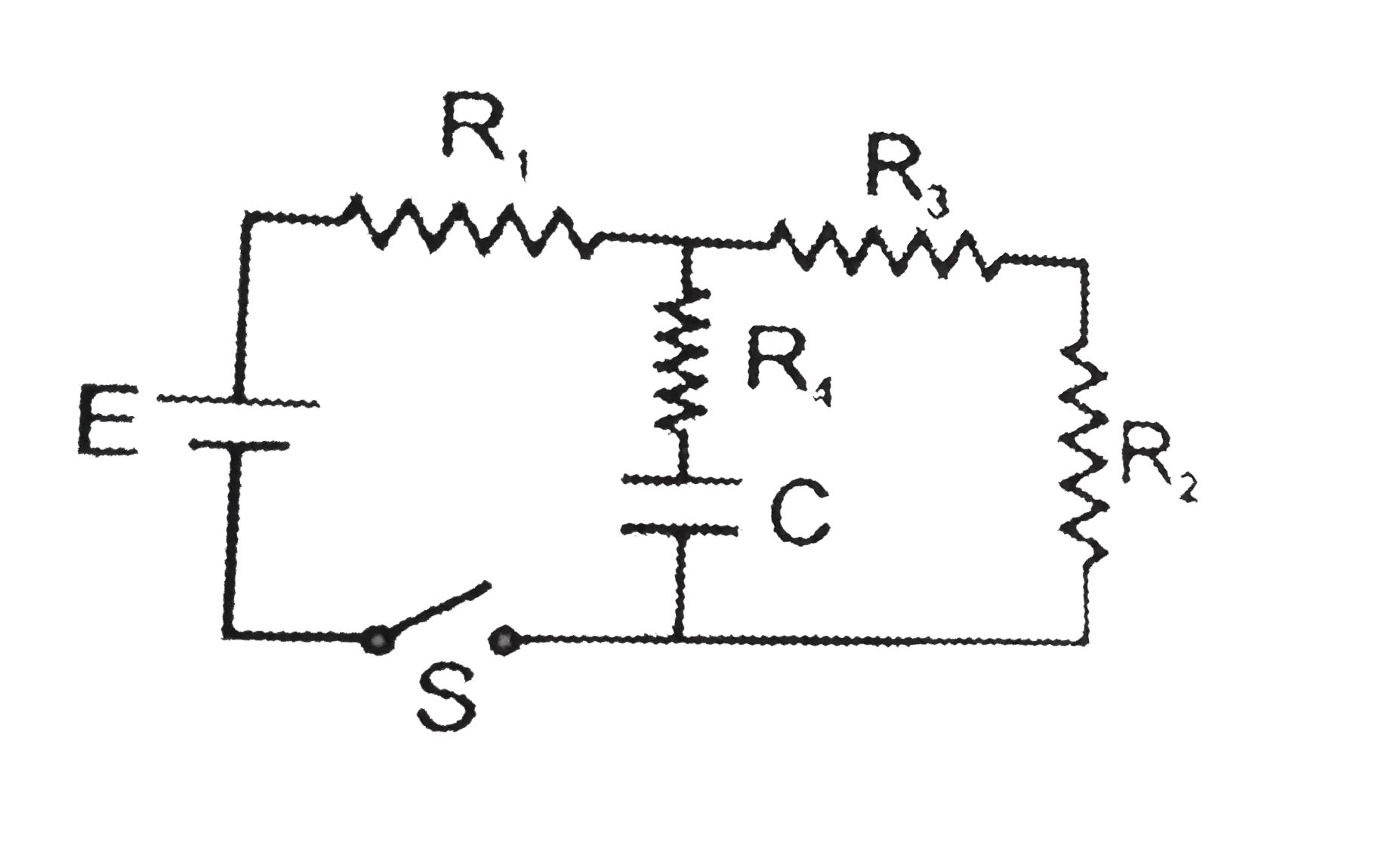
In the circuit shown in figure, The battery is an ideal one. With emf V. The capacitor is initially uncharged. The switch S is closed at time t=0.
(i) If Q(t)=CV2(1−e−xt3RC), find x.
If the liming value of current in AB at t→∞ is VxR, then find x.

The correct Answer is:(i) 2
(ii) 2
Let at any time t charge on capacitor C be Q and currents are if as shown, since,charge Q will increase with time t Therefore,
(i)Applying Kinchhoff's second law in loop MNABM
V=(i−i1)R+iRorV=2iR−i1R….(i)

Similarly,applying Kishhoff's second in loop MNSTM ,we have
V=i1R+QC+iR .....(ii)
Eliminating i from Eqs (i) and (ii), we get
V=3i1R+2Qcor3i1R=V−2Qc
or i1=13R(V−2QC)ordQdt=13R(V−2Qc)
or dQV−2QC=dt3Ror∫Q0dQV−2QC=∫t0dt3R
This equation given Q=CV2(1−e−2t/3RC) (ii)i1=dQdt=V3Re−2t/3RC
From Eq (i) i=V+i1R2R=V+V3e−2t/3RC2R∴ Current through AB
i2=i−i1=V+V3e−2t/3RC2R−v3Re−2t/3RC,i2=V2R−V6Re−2t/3RC

Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 39
1 Video
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 40
1 Video
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 37
1 Video
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Passage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
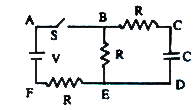
The current in the branch BE at t=∞ is
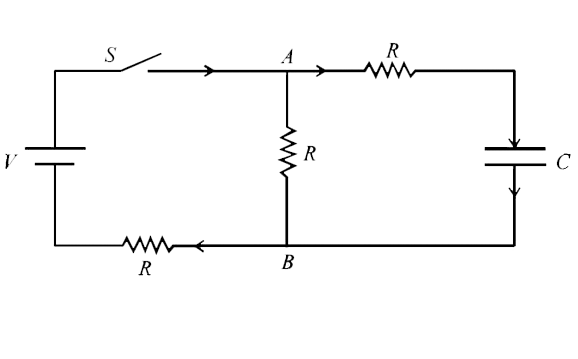
View SolutionIn the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
 .
.
View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
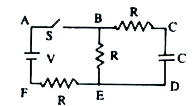
The current in branch containing capacitors at any time t is
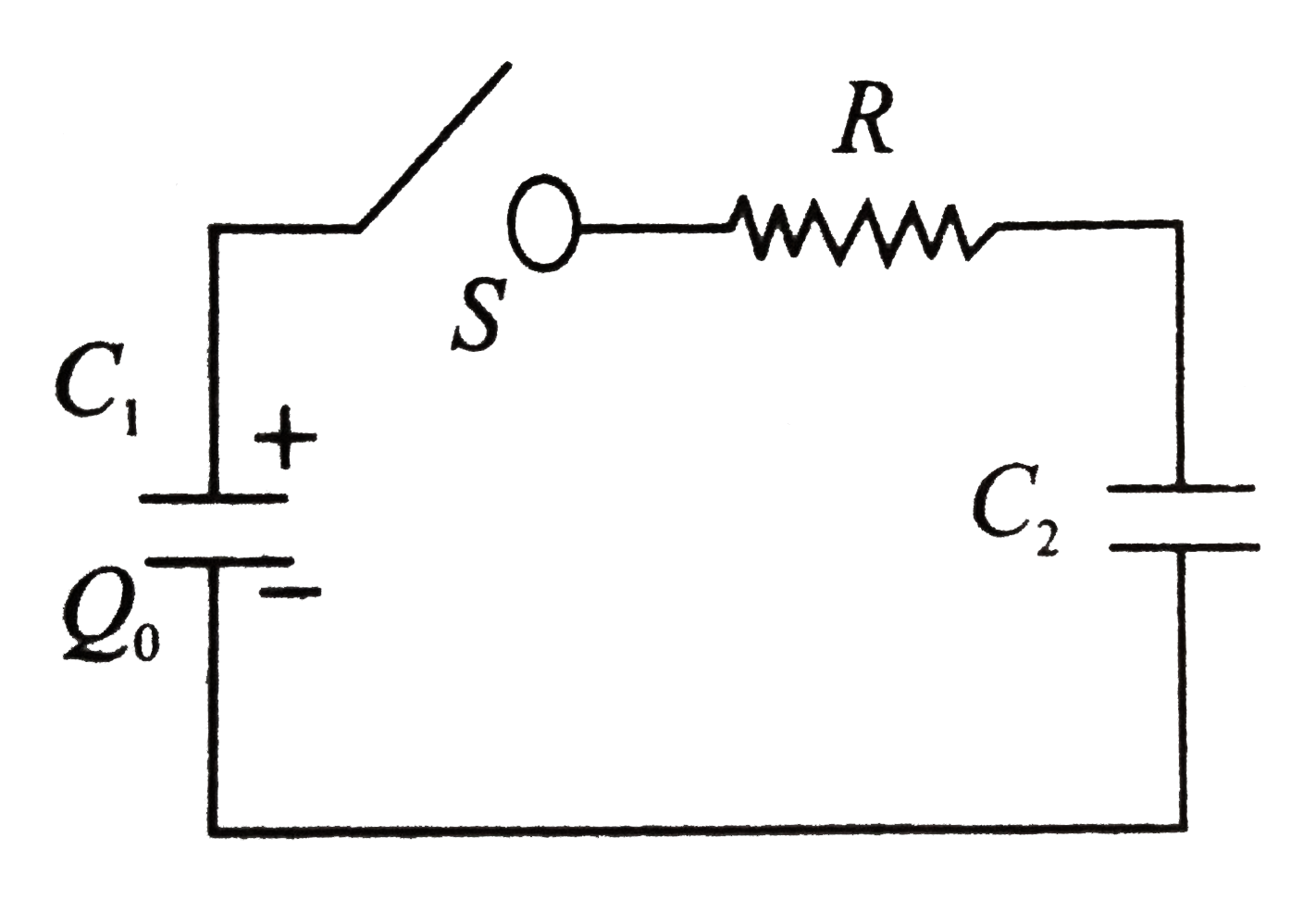
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

View SolutionIn the circuit shown in figure the switch S is closed at t = 0. A long time after closing the switch
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then capacitor is initially uncharged. Then the current through the resistor R=8Ω at t=0.4×10−3sec is (Take e−2=0.135 )

View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn the circuit shown in figure switch S is closed at time t=0. The charge which passes through the battery in one time constant is

View Solution