Question

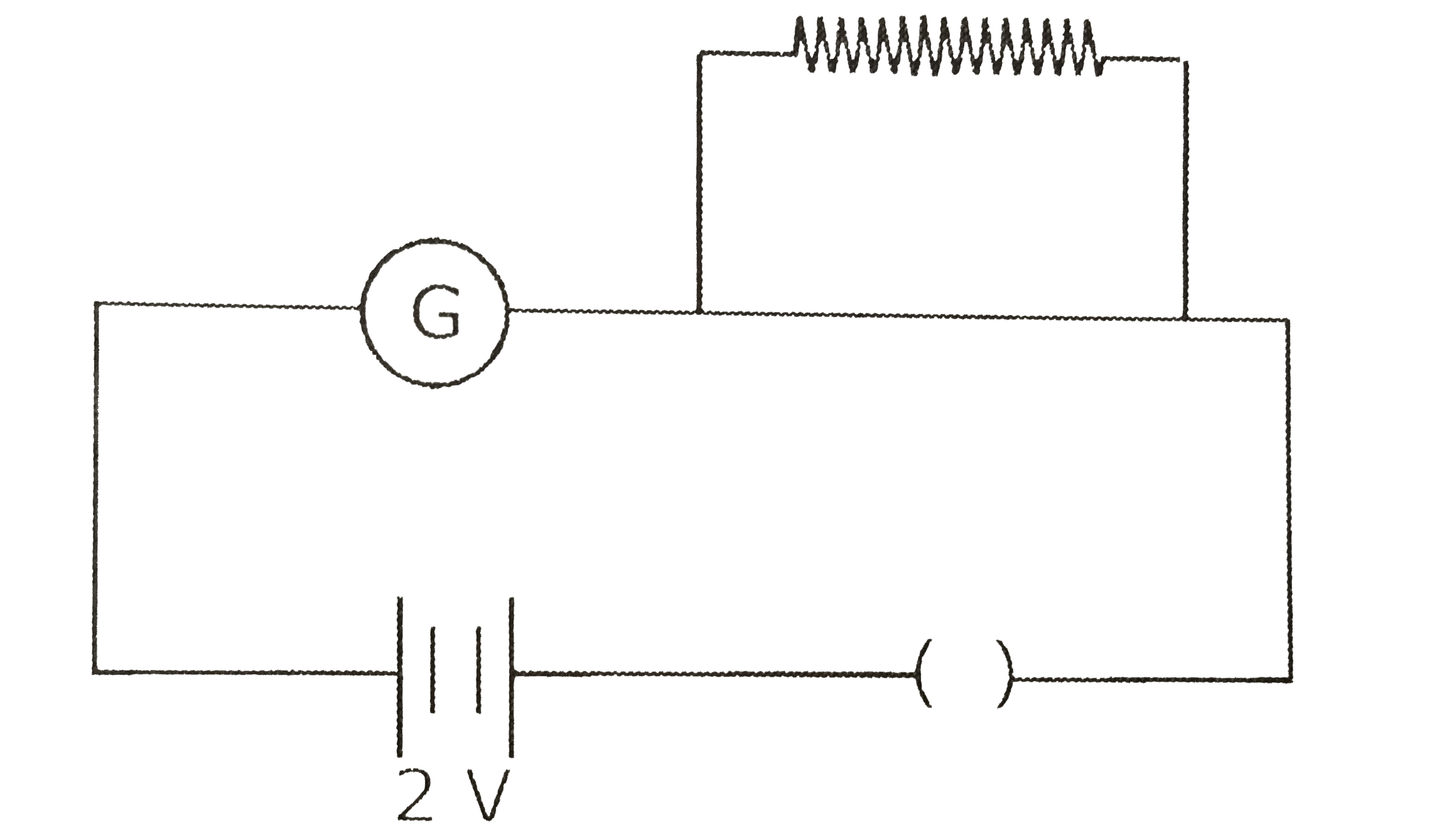
A galvanometer has a 50 division scale. Bat- tery has no internal resistance. It is found that there is deflection of 40 divisions when $R=2400\Omega$ . Deflection becomes 20 divisions when resistance taken from resistance box is $4900\Omega$. Then we can conclude :

Options

A. Current sensitivity of galvanometer is 20 mA/division.
B. Resistance of galvanometer is `200 Omega`
C. Resistance required on R.B. for a deflection of 10 divisions is `9800 Omega`
D. Full scale deflection current is 2 mA.

Answer

A

Explanation

The circuit given in the question is incorrect. The given figure shows the correct circuit. Let the current which produces full scale deflection in the galvanometer be `I_(g)` . Then according to questions.

`4/5I_(g)=V/(G+R)=2/(G+2400)` ...............i
`2/5I_(g)=2/(G+400)` ..............ii
From eqn (i) and (ii) `4/2=(G+4900)/(G+2400)=G=100Omega`, Putting G i Eq (i)
`4/5I_(g)=2/(100+2400)impliesI_(g)=(2xx5)/(2500)implies1mA` , For a deflectiion of 10 divisions
`1/5 I_(g)=V/(G+R)implies1/5xx10^(-3)=2/(100+R)impliesR=9900Omega`
Now current sensitivity `=(I_(g))/n=(1mA)/(50 diy)=20muA/` division