The vertices of a triangle are
,, .
Find the orthocentre of the triangle.
The correct Answer is:
To find the orthocenter of the triangle with vertices given by the coordinates (at1t2,a(t1+t2)), (at2t3,a(t2+t3)), and (at3t1,a(t3+t1)), we will follow these steps:
Step 1: Identify the vertices
Let:
- Vertex A: A(at1t2,a(t1+t2))
- Vertex B: B(at2t3,a(t2+t3))
- Vertex C: C(at3t1,a(t3+t1))
Step 2: Find the slope of line BC
The slope mBC of line segment BC can be calculated using the formula:
mBC=y2−y1x2−x1
Substituting the coordinates of points B and C:
mBC=a(t2+t3)−a(t3+t1)at2t3−at3t1
This simplifies to:
mBC=a(t2−t1)a(t2t3−t3t1)=t2−t1t2t3−t3t1
Step 3: Find the slope of line AC
Similarly, the slope mAC of line segment AC is:
mAC=a(t1+t2)−a(t3+t1)at1t2−at3t1
This simplifies to:
mAC=a(t2−t3)a(t1t2−t3t1)=t2−t3t1t2−t3t1
Step 4: Find the slope of the altitude from A to BC
The slope of the altitude from A to line BC, which is perpendicular to BC, is given by:
maltitudeA=−1mBC=−t2t3−t3t1t2−t1
Step 5: Write the equation of the altitude from A
Using point-slope form, the equation of the altitude from A is:
y−a(t1+t2)=maltitudeA(x−at1t2)
Step 6: Find the slope of the altitude from B to AC
Similarly, the slope of the altitude from B to line AC is:
maltitudeB=−1mAC=−t1t2−t3t1t2−t3
Step 7: Write the equation of the altitude from B
The equation of the altitude from B is:
y−a(t2+t3)=maltitudeB(x−at2t3)
Step 8: Solve the equations of the altitudes
To find the orthocenter, we need to solve the two equations obtained from the altitudes. By substituting and eliminating y, we can find the x coordinate of the orthocenter.
Step 9: Substitute back to find y
Once we have x, substitute it back into one of the altitude equations to find the corresponding y coordinate.
Final Result
After performing the calculations, we find that the orthocenter H of the triangle has coordinates:
H(−a,a(t1+t2+t3+t1t2t3))
Let:
- Vertex A: A(at1t2,a(t1+t2))
- Vertex B: B(at2t3,a(t2+t3))
- Vertex C: C(at3t1,a(t3+t1))
The slope mBC of line segment BC can be calculated using the formula:
mBC=y2−y1x2−x1
Substituting the coordinates of points B and C:
mBC=a(t2+t3)−a(t3+t1)at2t3−at3t1
This simplifies to:
mBC=a(t2−t1)a(t2t3−t3t1)=t2−t1t2t3−t3t1
Similarly, the slope mAC of line segment AC is:
mAC=a(t1+t2)−a(t3+t1)at1t2−at3t1
This simplifies to:
mAC=a(t2−t3)a(t1t2−t3t1)=t2−t3t1t2−t3t1
The slope of the altitude from A to line BC, which is perpendicular to BC, is given by:
maltitudeA=−1mBC=−t2t3−t3t1t2−t1
Using point-slope form, the equation of the altitude from A is:
y−a(t1+t2)=maltitudeA(x−at1t2)
Similarly, the slope of the altitude from B to line AC is:
maltitudeB=−1mAC=−t1t2−t3t1t2−t3
The equation of the altitude from B is:
y−a(t2+t3)=maltitudeB(x−at2t3)
To find the orthocenter, we need to solve the two equations obtained from the altitudes. By substituting and eliminating y, we can find the x coordinate of the orthocenter.
Once we have x, substitute it back into one of the altitude equations to find the corresponding y coordinate.
After performing the calculations, we find that the orthocenter H of the triangle has coordinates:
H(−a,a(t1+t2+t3+t1t2t3))
Topper's Solved these Questions
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Archive (Analytical and Descriptive Questions:)
4 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Archive (Match the column:)
1 Videos
- STRAIGHT LINESBOOK - VMC MODULES ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - JEE Main Archive (State true or false: Q. 16 to 18)
3 Videos
- SEQUENCE AND SERIES BOOK - VMC MODULES ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - JEE MAIN & Advance ( ARCHIVE)
46 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - VMC MODULES ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - JEE ADVANCED (ARCHIVE)
34 Videos
Similar Questions
The vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionFind the area of that triangle whose vertices are (at21,2at1),(at22,2at2)and(at23,2at3).
View SolutionIf O is the orthocentre of triangle ABC whose vertices are at A(at21,2at1,B(at22,2at2)andC(at23,2at3) then the coordinates of the orthocentreof ΔO'BC are
View Solution
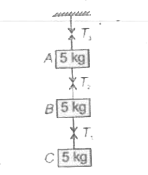
Calculate a, T1,T2,T1'&T2'.
View SolutionIf a circle intersects the parabola y2=4ax at points A(at21,2at1),B(at22,2at2),C(at23,2at3),D(at24,2at4), then t1+t2+t3+t4 is
View SolutionThe area of triangle formed by tangents at the parametrie points t1,t2 and t3, on y2=4ax is k|(t1−t2)(t2−t1)(t3−t1)| then K =
View SolutionThe value of T3T1 is
View SolutionIf t1,t2andt3 are distinct, the points (t12at1+at31),(t2,2at2+at32)and(t3,2at3+at33)
View SolutionFind the distance between the points (at21,2at1) and (at22,2at2), where t1 and t2 are the roots of the equation x2−2√3x+2=0 and a>0.
View Solution
