1c∫bcacf(xc)dx=
c∫baf(cx)dx
1c∫baf(xc)dx
1c∫baf(cx)dx
c∫baf(xc)dx
The correct Answer is:A
To solve the integral
1c∫bcacf(xc)dx,
we will perform a substitution to simplify the expression.
Step 1: Substitute t=xc
Let t=xc. Then, we can express x in terms of t:
x=ct.
Step 2: Differentiate to find dx
Differentiating both sides with respect to t:
dx=cdt.
Step 3: Change the limits of integration
Now, we need to change the limits of integration. When x=ac:
t=acc=a.
When x=bc:
t=bcc=b.
Step 4: Substitute into the integral
Now substitute x and dx in the integral:
1c∫bcacf(xc)dx=1c∫baf(t)⋅(cdt).
Step 5: Simplify the expression
The c in the numerator and denominator cancels out:
=∫baf(t)dt.
Step 6: Change t back to x
Since t was just a substitution, we can rename it back to x:
=∫baf(x)dx.
Final Result
Thus, we conclude that:
1c∫bcacf(xc)dx=∫baf(x)dx.
Conclusion
The correct answer is option d:
∫baf(x)dx.
Topper's Solved these Questions
- INTEGRAL CALCULUS - 2 BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Main (Archive)
64 Videos
- INTEGRAL CALCULUS - 2 BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Advanced (Archive)
103 Videos
- INTEGRAL CALCULUS - 2 BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS - 2 EXERCISE - JEE Advanced (Archive)
103 Videos
- FUNCTIONSBOOK - VMC MODULES ENGLISHCHAPTER - FUNCTIONSEXERCISE - JEE Main & Advanced
8 Videos
- INTEGRAL CALCULUS-1BOOK - VMC MODULES ENGLISHCHAPTER - INTEGRAL CALCULUS-1EXERCISE - JEE ADVANCED (ARCHIVE)
25 Videos
Similar Questions
Knowledge Check
∫b+ca+cf(x)dx is equal to
A∫baf(x−c)dxB∫baf(x+c)dxC∫baf(x)dxD∫b−ca−cf(x)dx
STATEMENT-1 : ∫5π−2πcot−1(tanx)dx=7π22
and
STATEMENT-2 : ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx, a<c<b
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
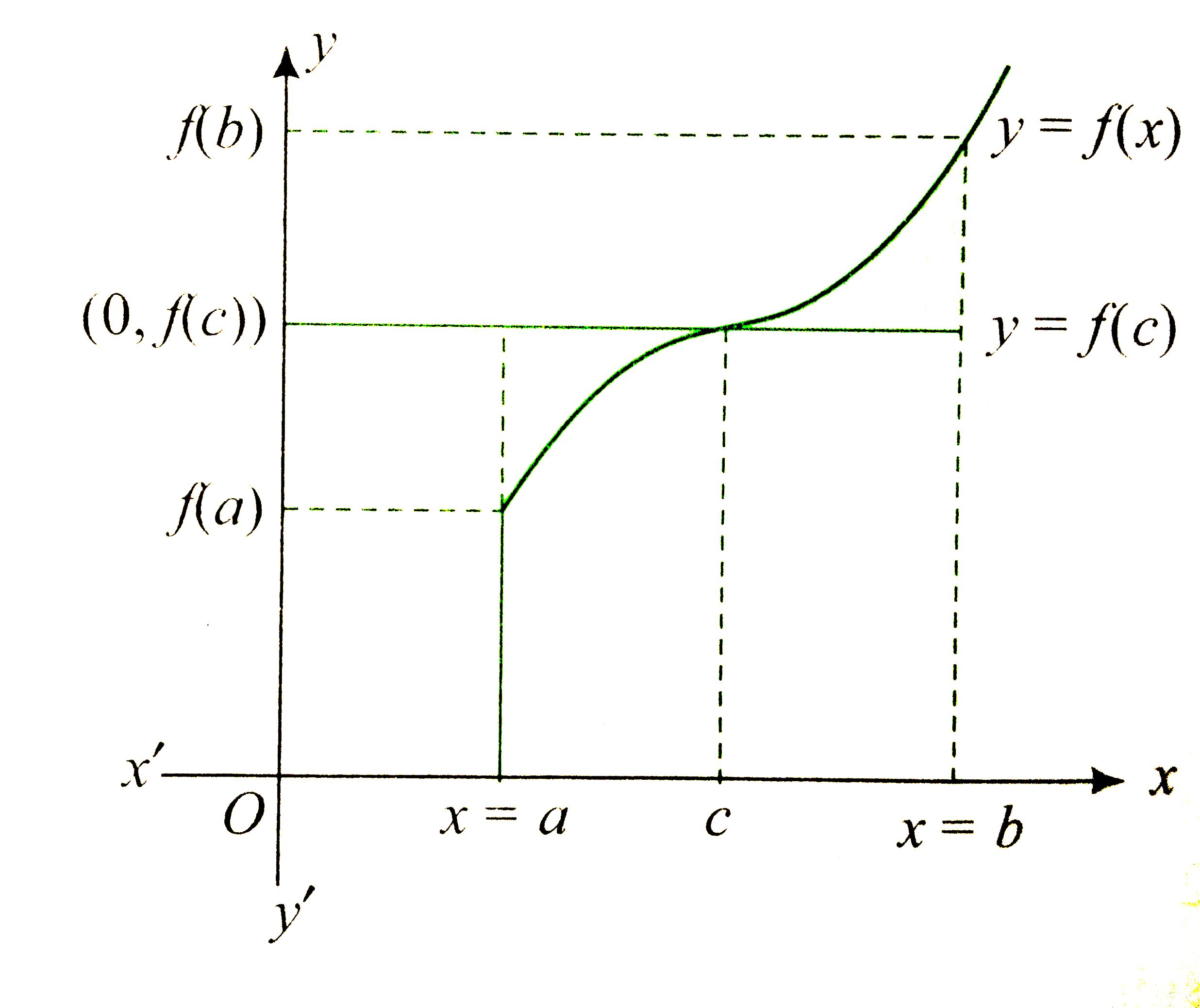
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
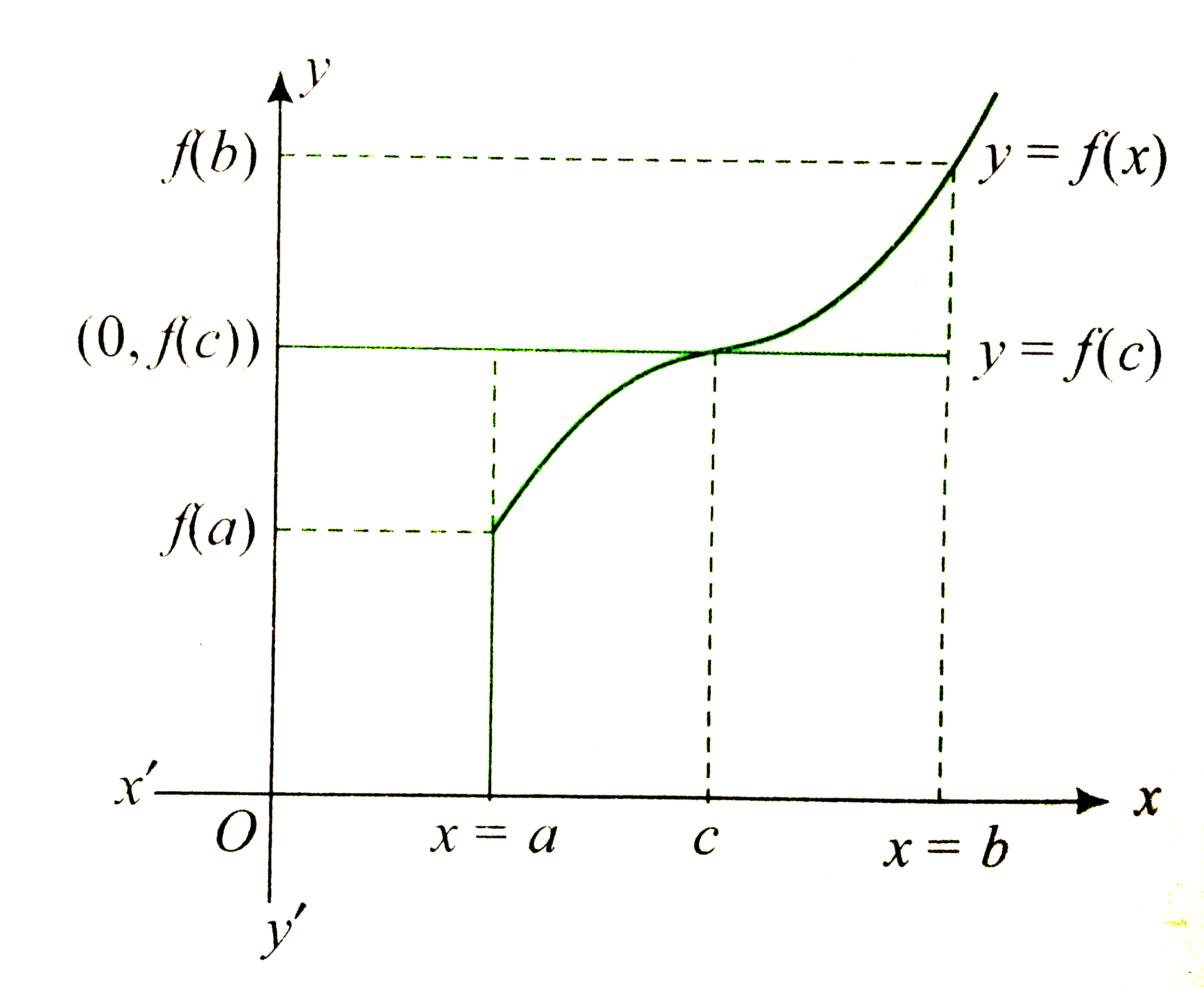
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
View SolutionProve that ∫baf(x)dx=∫b+ca+cf(x−c)dx , and when f(x) is odd function, ∫a−af(x)dx=0
View SolutionLet the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal to
View SolutionIf a<b<c∈R and f(a+b+c−x)=f(x) for all, x then ∫bax(f(x)+f(x+c))dxa+b is:
View SolutionIf f(x) is a continuous function ∀x∈R, then which of the following is (are) true, (a)∫164f(√x)dx=4cf(c) for some c∈(2,4) (b)∫164f(√x)dx=4cf(c) for some c∈(2,16) (c)∫164f(√x)dx=6(2−cf′(c)) for some c∈(4,16), if f(2)=f(4) (d)∫164f(√x)dx=6(2−cf′(c)) for some c∈(2,4), if f(2)=f(4)
View Solution
