The differential equation of the family of curves y=ex(Acosx+Bsinx), where A and B are arbitrary constants is (a) (b)(c)(d)(e)(f)d(g)2(h)(i)yj((k)d(l)x(m)2(n)(o))(p)(q)−2(r)(s)dyt((u)dx)(v)(w)+2y=0(x) (y) (z) ( a a ) (bb) (cc)(( d d ) (ee) d^(( f f )2( g g ))( h h ) y)/( i i )(( j j ) d (kk) x^(( l l )2( m m ))( n n ))( o o ) (pp)+2( q q )(( r r ) dy)/( s s )(( t t ) dx)( u u ) (vv)+2y=0( w w ) (xx) (yy) ( z z ) (aaa) (bbb)(( c c c ) (ddd) d^(( e e e )2( f f f ))( g g g ) y)/( h h h )(( i i i ) d (jjj) x^(( k k k )2( l l l ))( m m m ))( n n n ) (ooo)+( p p p ) (qqq)(( r r r ) (sss) (ttt)(( u u u ) dy)/( v v v )(( w w w ) dx)( x x x ) (yyy) (zzz))^(( a a a a )2( b b b b ))( c c c c )+y=0( d d d d ) (eeee) (ffff) ( g g g g ) (hhhh) (iiii)(( j j j j ) (kkkk) d^(( l l l l )2( m m m m ))( n n n n ) y)/( o o o o )(( p p p p ) d (qqqq) x^(( r r r r )2( s s s s ))( t t t t ))( u u u u ) (vvvv)-7( w w w w )(( x x x x ) dy)/( y y y y )(( z z z z ) dx)( a a a a a ) (bbbbb)+2y=0( c c c c c ) (ddddd)
d2ydx2+2dydx+2y=0
d2ydx2−2dydx+2y=0
d2ydx2−2dydx−2y=0
none of these
The correct Answer is:B
To find the differential equation of the family of curves given by y=ex(Acosx+Bsinx), where A and B are arbitrary constants, we will follow these steps:
Step 1: Differentiate y with respect to x
Given:
y=ex(Acosx+Bsinx)
We will differentiate y with respect to x using the product rule:
dydx=ex(Acosx+Bsinx)′+(ex)′(Acosx+Bsinx)
Calculating the derivatives:
(Acosx+Bsinx)′=−Asinx+Bcosx
So,
dydx=ex(−Asinx+Bcosx)+ex(Acosx+Bsinx)
This simplifies to:
dydx=ex(Bcosx−Asinx+Acosx+Bsinx)=ex((B+A)cosx+(B−A)sinx)
Step 2: Differentiate dydx to find d2ydx2
Now we differentiate dydx:
d2ydx2=ddx(ex((B+A)cosx+(B−A)sinx))
Using the product rule again:
d2ydx2=ex((B+A)cosx+(B−A)sinx)′+(ex)′((B+A)cosx+(B−A)sinx)
Calculating the derivative:
((B+A)cosx+(B−A)sinx)′=−(B+A)sinx+(B−A)cosx
So,
d2ydx2=ex(−(B+A)sinx+(B−A)cosx)+ex((B+A)cosx+(B−A)sinx)
This simplifies to:
d2ydx2=ex((B−A)cosx−(B+A)sinx+(B+A)cosx+(B−A)sinx)
Combining like terms:
d2ydx2=ex(2Bcosx+2Asinx)
Step 3: Substitute back to eliminate A and B
From the original equation, we can express A and B in terms of y and its derivatives. We have:
y=ex(Acosx+Bsinx)
This gives us:
Acosx+Bsinx=yex
Using the expressions for dydx and d2ydx2, we can eliminate A and B to form a differential equation.
Step 4: Form the differential equation
We can rearrange the terms to get:
d2ydx2−2dydx+2y=0
Thus, the differential equation of the family of curves is:
d2ydx2−2dydx+2y=0
Final Answer
The differential equation of the family of curves is:
d2ydx2−2dydx+2y=0
Given:
y=ex(Acosx+Bsinx)
We will differentiate y with respect to x using the product rule:
dydx=ex(Acosx+Bsinx)′+(ex)′(Acosx+Bsinx)
Calculating the derivatives:
(Acosx+Bsinx)′=−Asinx+Bcosx
So,
dydx=ex(−Asinx+Bcosx)+ex(Acosx+Bsinx)
This simplifies to:
dydx=ex(Bcosx−Asinx+Acosx+Bsinx)=ex((B+A)cosx+(B−A)sinx)
Now we differentiate dydx:
d2ydx2=ddx(ex((B+A)cosx+(B−A)sinx))
Using the product rule again:
d2ydx2=ex((B+A)cosx+(B−A)sinx)′+(ex)′((B+A)cosx+(B−A)sinx)
Calculating the derivative:
((B+A)cosx+(B−A)sinx)′=−(B+A)sinx+(B−A)cosx
So,
d2ydx2=ex(−(B+A)sinx+(B−A)cosx)+ex((B+A)cosx+(B−A)sinx)
This simplifies to:
d2ydx2=ex((B−A)cosx−(B+A)sinx+(B+A)cosx+(B−A)sinx)
Combining like terms:
d2ydx2=ex(2Bcosx+2Asinx)
From the original equation, we can express A and B in terms of y and its derivatives. We have:
y=ex(Acosx+Bsinx)
This gives us:
Acosx+Bsinx=yex
Using the expressions for dydx and d2ydx2, we can eliminate A and B to form a differential equation.
We can rearrange the terms to get:
d2ydx2−2dydx+2y=0
d2ydx2−2dydx+2y=0
The differential equation of the family of curves is:
d2ydx2−2dydx+2y=0
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:LEVEL -2
Explore 39 Videos
- DIFFERENTIAL EQUATIONSBook:VMC MODULES ENGLISHChapter:DIFFERENTIAL EQUATIONSExercise:NUMERICAL VALUE TYPE FOR JEE MAIN
Explore 11 Videos
- DIFFERENTIAL CALCULUS 2Book:VMC MODULES ENGLISHChapter:DIFFERENTIAL CALCULUS 2Exercise:JEE Advanced (Archive)
Explore 81 Videos
- FUNCTIONSBook:VMC MODULES ENGLISHChapter:FUNCTIONSExercise:JEE Main & Advanced
Explore 8 Videos
Similar Questions
The equation of curves which intersect the hyperbola xy=4 at an angle π2 is
View SolutionIf y= y(x) 2cosxy+1(dydx)=−sinx,y(0)=1 then y(π2) equal ____.
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
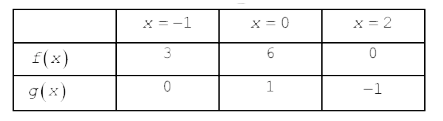
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionLet f(x)=sin(π6sin(π2sinx)) for all x∈Randg(x)=π2sinx for all x∈R. Let (fog)(x) denote f(g(x))and(gof)(x) denote g(f(x)). Then which of the following is (are) true?
View SolutionA B C D E F G H I J K L M N O P Q R S T U V W X Y Z
AZ, CX, FU, ….
View SolutionA B C D E F G H I J K L M N O P Q R S T U V W X Y Z
BDF, CFI, DHL, ….
View SolutionA B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A, CD, GHI, …., UVWXY
View SolutionSolution of dydx+2xy=y is (a) (b)(c)y=c(d)ee(f)x−(g)x((h)2(i))(j)(k)(l)(m) (n) (b) (o)(p)y=c(q)er(s)(t)x((u)2(v))(w)−x(x)(y)(z) (aa) (c) (d)(e)y=c(f)e(g)x(h)(i)(j) (k) (d) (l)(m)y=c(n)eo(p)−(q)x((r)2(s))(t)(u)(v)(w) (x)
View SolutionThe differential equation of all non-horizontal lines in a plane is (a) (b)(c)(d)(e)(f)d(g)2(h)(i)yj((k)d(l)x(m)2(n)(o))(p)(q)(r) (s) (b) (t)(u)(v)(w)(x)d(y)2(z)(aa)xbb((cc)d(dd)y(ee)2(ff)(gg))(hh)(ii)=0(jj) (kk) (c) (d)(e)(f)(g)dyh((i)dx)(j)(k)=0(l) (m) (d) (n)(o)(p)(q)dxr((s)dy)(t)(u)=0(v) (w)
View SolutionDifferential equation of the family of circles touching the line y=2 at (0,2) is (a) (b)(c)(d)x(e)2(f)(g)+(h)(i)((j)(k)y−2(l))(m)2(n)(o)+(p)(q)dyr((s)dx)(t)(u)((v)(w)y−2(x))=0(y) (z) (aa) ( b b ) (cc) (dd) x^(( e e )2( f f ))( g g )+(( h h ) (ii) y-2( j j ))(( k k ) (ll)2-2x (mm)(( n n ) dx)/( o o )(( p p ) dy)( q q ) (rr)-y (ss))=0( t t ) (uu) (vv) (ww)(×)(yy)x(zz)2(aaa)(bbb)+(ccc)(ddd)((eee)(fff)y−2(ggg))(hhh)2(iii)(jjj)+((kkk)(lll)(mmm)(nnn)dxooo((ppp)dy)(qqq)(rrr)+y−2(sss))((ttt)(⋃)y−2(vvv))=0(www) (xxx) (yyy) None of these
View SolutionThe differential equation whose general solution is given by y=(c1cos(x+c2)−(c3e(−x+c4)+(c5sinx), where c1,c2,c3,c4,c5 are arbitrary constants, is (a) (b)(c)(d)(e)(f)d(g)4(h)(i)yj((k)d(l)x(m)4(n)(o))(p)(q)−(r)(s)(t)d(u)2(v)(w)yx((y)d(z)x(aa)2(bb)(cc))(dd)(ee)+y=0(ff) (gg) (hh) (ii)(jj)(kk)(ll)(mm)d(nn)3(oo)(pp)yqq((rr)d(ss)x(tt)3(uu)(vv))(ww)(×)+(yy)(zz)(aaa)d(bbb)2(ccc)(ddd)yeee((fff)d(ggg)x(hhh)2(iii)(jjj))(kkk)(lll)+(mmm)(nnn)dyooo((ppp)dx)(qqq)(rrr)+y=0(sss) (ttt) (uuu) (vvv)(www)(×x)(yyy)(zzz)d(aaaa)5(bbbb)(cccc)dddd((eeee)d(ffff)x(gggg)5(hhhh)(iiii))(jjjj)(kkkk)+y=0(llll) (mmmm) (nnnn) (oooo)(pppp)(qqqq)(rrrr)(ssss)d(tttt)3(uuuu)(vvvv)ywwww((xxxx)d(yyyy)x(zzzz)3(aaaaa)(bbbbb))(ccccc)(ddddd)−(eeeee)(fffff)(ggggg)d(hhhhh)2(iiiii)(jjjjj)ykkkkk((lllll)d(mmmmm)x(nnnnn)2(ooooo)(ppppp))(qqqqq)(rrrrr)+(sssss)(ttttt)dyuuuuu((vvvvv)dx)(wwwww)(××x)−y=0(yyyyy) (zzzzz)
View SolutionThe solution of the differential equation x=1+xydydx+x2y22!(dyd)2+x3y33!(dydx)3+is (a) (b)(c)y=1n((d)x(e))+c(f) (g) (b) (h)(i)(j)y(k)2(l)(m)=(n)(o)((p)(q)1nx(r))(s)2(t)(u)+c(v) (w) (c) (d)(e)y=logx+xy(f) (g) (d) (h)(i)xy=(j)x(k)y(l)(m)+c(n) (o)
View SolutionThe solution of (y+x+5)dy=(y−x+1)dx is (a) ( b ) (c)log(( d ) (e) (f) (g)(( h ) (i) y+3( j ))^(( k )2( l ))( m )+( n ) (o)(( p ) (q) x+2( r ))^(( s )2( t ))( u ) (v))+( w ) (x)tan^(( y ) (z)-1( a a ))( b b ) (cc)(( d d ) y+3)/( e e )(( f f ) y+2)( g g ) (hh)+C (ii) (jj) (kk) (ll)(mm)log((nn)(∞)(pp)(qq)((rr)(ss)y+3(tt))(uu)2(vv)(ww)+(xx)(yy)((zz)(aaa)x−2(bbb))(ccc)2(ddd)(eee)(fff))+(ggg)(hhh)tan(iii)(jjj)−1(kkk)(lll)(mmm)(nnn)y−3ooo((ppp)y−2)(qqq)(rrr)+C(sss) (ttt) (uuu) ( v v v ) (www)log(( x x x ) (yyy) (zzz) (aaaa)(( b b b b ) (cccc) y+3( d d d d ))^(( e e e e )2( f f f f ))( g g g g )+( h h h h ) (iiii)(( j j j j ) (kkkk) x+2( l l l l ))^(( m m m m )2( n n n n ))( o o o o ) (pppp))+2( q q q q ) (rrrr)tan^(( s s s s ) (tttt)-1( u u u u ))( v v v v ) (wwww)(( x x x x ) y+3)/( y y y y )(( z z z z ) x+2)( a a a a a ) (bbbbb)+C (ccccc) (ddddd) (eeeee) ( f f f f f ) (ggggg)log(( h h h h h ) (iiiii) (jjjjj) (kkkkk)(( l l l l l ) (mmmmm) y+3( n n n n n ))^(( o o o o o )2( p p p p p ))( q q q q q )+( r r r r r ) (sssss)(( t t t t t ) (uuuuu) x+2( v v v v v ))^(( w w w w w )2( x x x x x ))( y y y y y ) (zzzzz))-2( a a a a a a ) (bbbbbb)tan^(( c c c c c c ) (dddddd)-1( e e e e e e ))( f f f f f f ) (gggggg)(( h h h h h h ) y+3)/( i i i i i i )(( j j j j j j ) x+2)( k k k k k k ) (llllll)+C (mmmmmm) (nnnnnn)
View SolutionThe solution of the differential equation dydx=3x2y4+2xyx2−2x3y3 is (a) (b)(c)(d)(e)(f)y(g)2(h)(i)jx(k)(l)−(m)x(n)3(o)(p)(q)y(r)2(s)(t)=c(u) (v) (w) ( x ) (y) (z)(( a a ) (bb) x^(( c c )2( d d ))( e e ))/( f f )(( g g ) (hh) y^(( i i )2( j j ))( k k ))( l l ) (mm)+( n n ) x^(( o o )3( p p ))( q q ) (rr) y^(( s s )3( t t ))( u u )=c (vv) (ww) (xx) (yy)(zz)(aaa)(bbb)(c)x(ddd)2(eee)(fff)gggy(hhh)(iii)+(jjj)x(kkk)3(lll)(mmm)(⋂)y(ooo)2(ppp)(qqq)=c(rrr) (sss) (d) (ttt)(⋃)(⋁)(www)(×x)x(yyy)2(zzz)(aaaa)bbbb((cccc)3y)(dddd)(eeee)−2(ffff)x(gggg)3(hhhh)(iiii)(jjjj)y(kkkk)2(llll)(mmmm)=c(⋂n) (oooo)
View SolutionThe solution of the differential equation {1+x√(x2+y2)}dx+{√(x2+y2)−1}ydy=0 is equal to (a) (b)(c)(d)x(e)2(f)(g)+(h)(i)(j)y(k)2(l)(m)n2(o)(p)+(q)1r3(s)(t)(u)(v)((w)(x)(y)x(z)2(aa)(bb)+(cc)y(dd)2(ee)(ff)(gg))(hh)(ii)(jj)3kk2(ll)(mm)(∩)(oo)=c(pp) (qq) (rr) ( s s ) (tt) x+( u u )(( v v ) (ww) y^(( x x )3( y y ))( z z ))/( a a a )3( b b b ) (ccc)+( d d d )1/( e e e )2( f f f ) (ggg) (hhh) (iii)(( j j j ) (kkk) (lll) x^(( m m m )2( n n n ))( o o o )+( p p p ) y^(( q q q )2( r r r ))( s s s ) (ttt))^(( u u u ) (vvv) (www)1/( x x x )2( y y y ) (zzz) (aaaa))( b b b b )=c (cccc) (dddd) (eeee) ( f f f f ) (gggg) x-( h h h h )(( i i i i ) (jjjj) y^(( k k k k )2( l l l l ))( m m m m ))/( n n n n )2( o o o o ) (pppp)+( q q q q )1/( r r r r )3( s s s s ) (tttt) (uuuu) (vvvv)(( w w w w ) (xxxx) (yyyy) x^(( z z z z )2( a a a a a ))( b b b b b )+( c c c c c ) y^(( d d d d d )2( e e e e e ))( f f f f f ) (ggggg))^(( h h h h h ) (iiiii) (jjjjj)3/( k k k k k )2( l l l l l ) (mmmmm) (nnnnn))( o o o o o )=c (ppppp) (qqqqq)
View Solution