Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

(i) If σ be the mass/unit area of the disc,
mass of the whole disc, m1=πR2σ
radius of the hold =R/2
mass of the hold, m2=π(R/2)2σ
distance of centre of mass of the hold from O, i.e., x2=R2
Since, the hole has been taken out, its mass is taken as negative.
If O is the origin,
xcm=m1x1−m2x2m1+m2=(πR2σ)×0−π(R/2)2σ×(R/2)πR2σ−π(R/2)2σ
=−πR2σ/8(3/4)πR2σ=−R6
The negative sign indicates that the CM is to the left of O.
(ii) When the block-2 is shifted to the left by a small distance x,Potential energy of compression of the spring,U=12kx2
As the block-1 break off the wall and the spring is unstretched, its potential energy is converted to kinetic energy of block-2 which acquires a velocity v2 , where
12m2v22=12kx2 or v2=√km2x
Since, both the block-I is initially at rest, v1=0.
If vcm is the velocity of the centre of mass of the system,
vcm=m1v1×m2v2m1+m2
=m1×+m2(k/m2)xm1+m2=(x√km2m1+m2)
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1
45 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Angular Momentum, Collision)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL-0 (SA-II Short Answer Type -II)
12 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
Choose the correct option:
Two bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The velocity of the centre of mass of the system when bar 1 breaks off the wall is
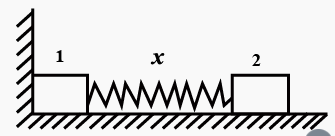
View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is

View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
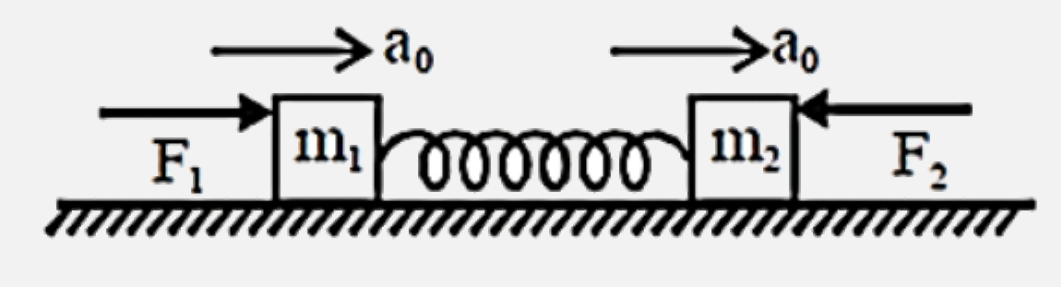
View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth plane .find the value of spring force .
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo block of masses m1andm2 are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .

(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
