In the Column-I below, four different paths of a particle are given as functions of time. In these functions, α and β are positive constants of appropriate dimensions and α≠β. In each case, the force acting on the particle is either zero or conservative. In Column-II, five physical quantities of the particle are mentioned: →p is the linear momentum, →L is the angular momentum about the origin, K is the kinetic energy, U is the potential energy and E is the total energy. Match each path in Column-I with those quantities in Column-II, which are conserved for that path:

A-PQRST, B-Q,T, C-Q,R,S,T, D-T
A=P,Q,R,S,T, B=R,T, C=C,Q,R,S,T, D=Q,T
A=Q,R,S, B=T, C=P,Q,S, D=Q,T
A=P,Q,R,T, B=Q,T, C=Q,R,S,T, D=Q,T
The correct Answer is:A
A. →r=αtˆi+βtˆj
→v=αˆi+βˆj
→a=0⇒→F=0
∴A−P,Q−R,S,T
B. →r=αcosωθi+βsinωtˆj, →v=−αωsinωtˆi+βωcosωtˆj
→a=−αω2cosωthai−βω2sinωtˆj,→a=−ω2→r⇒ Force is towards centre
→a.→v=(α2−β2)ω3sinωtcosωt≠0
⇒ Work is done by the force and kinetic energy of particle will not be conserved.
∴B−Q,T
C. →r=αcosωtˆi+αsinωtˆj
⇒ Uniform circular motion, ∴ C,Q,R,S,T
D. →r=αtˆi+β2t2ˆj, →v=αˆi+βtˆj
→a=βˆj⇒ force is not passing through origin ∴ D-T
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
Explore 15 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)
Explore 14 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (ASSERTION & REASON TYPE)
Explore 2 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.
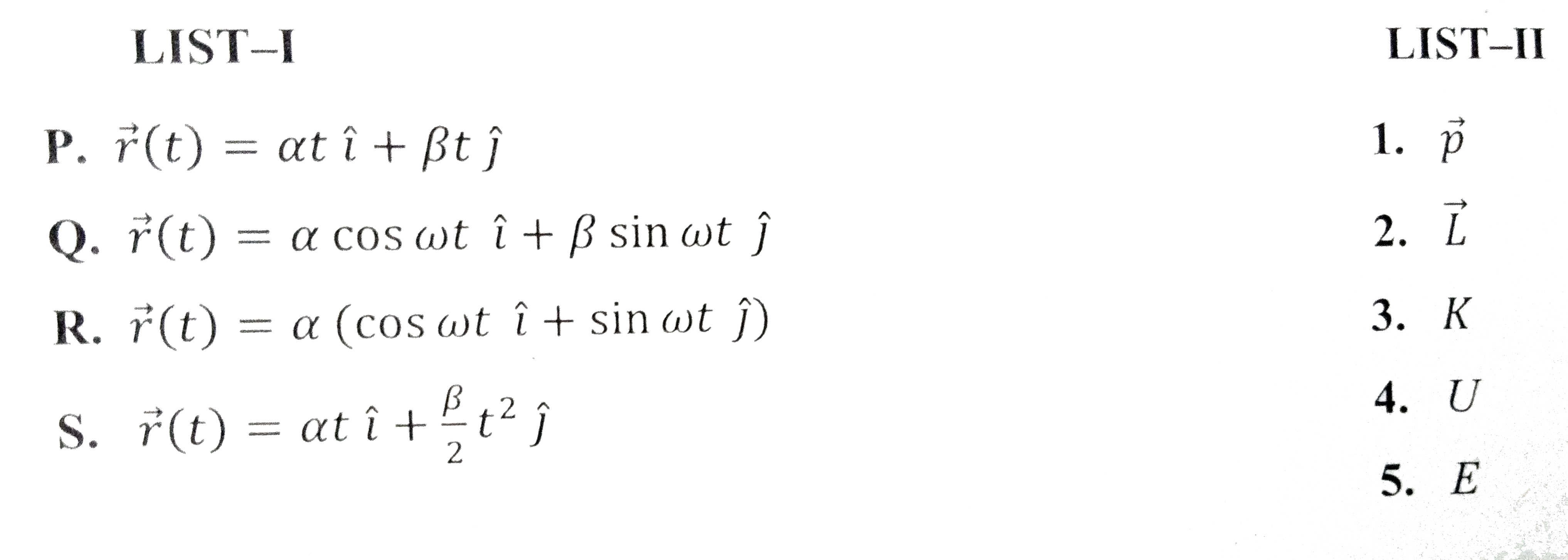
View SolutionMatch the units/dimensions in Column-I with the physical quantities in column -II :

View Solution
Knowledge Check
The linear momentum p of a particle is given as a function of time t as p=At2+Bt+C.The dimensions of constant B are
A[ML−1T−1]B[ML−1T−2]C[MLT−2]D[MLT−1]Figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
 AABBBCCCDDDE
AABBBCCCDDDEEnergy due to position of a particle is given by, U=α√yy+β, where α and β are constants, y is distance. The dimensions of (α×β) are
A[M0LT0]B[M1/2L3/2T−2]C[M0L−7/2T0]D[ML7/2T−2]
The linear momentum p of a particle is given as a function of time t as p=At2+Bt+C.The dimensions of constant B are
View Solutionα-particles and β-particles
View SolutionThe linear momentum of a particle as a fuction of time 't' is given by , p = a +bt , where a and b are positive constants . What is the force acting on the particle ?
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionEnergy due to position of a particle is given by, U=α√yy+β, where α and β are constants, y is distance. The dimensions of (α×β) are
View Solution
