The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Then why does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
The electrical energy of the atmosphere is dissipated during a lightning in the form of heat, sound and light energy.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (SHORT ANSWER TYPE )
27 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
The earth's surface has a negative surface charge density of 10−9Cm−2 . The potential difference of 400 kV between the top of the atmosphere and the surface results (due to low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmosphereic electric field , how much time (roughly) would be required to neutralise the earth's surface ? (This never happens in practice because there is a mechanism to replenish electric charges namely the continual thunder storms and lightning in different parts of the globe). Radius of the earth =6.37×106m.
View SolutionPositive and negative ions are produced in the atmosphere due to cosmic rays from space and also due to radioactive elements in the soil. In some region in the atmosphere, the electric field strength is 100V/m in the vertically downward direction. This field exerts force on the positive and negative ions in the given region in atmosphere. As a result, positive ions, having a density 500/cm3 drift downward while negative ions, having a density 300/cm3 drift upward. All these ions are singly charged. It is observed that the conductivity in the given region is 4×10−13(Ω−m)−1. Find the average speed of ions, assuming it to be the same for positive and negative ions.
View Solution
Knowledge Check
Environmentalist Otters
It has long been known that the sea otters (23) living along the West Coast of North America help––––––––––––––––––––––––––––––––––––––––––––––––––––––– keep kelp forests in their habitat healthy and vital. They do this by feeding on sea urchins and other herbivorous invertebrates that graze voraciously on kelp. With sea otters to keep the population of sea urchins in check, kelp forests can flourish. In fact, (24) two years or less of sea otters can completely eliminate sea urchins––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– in a coastal area (see chart).
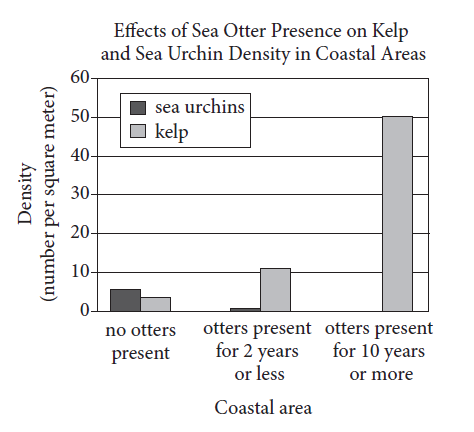
Adapted from David O. Duggins, “Kelp Beds and Sea Otters: An Experimental Approach.” ©1980 by the Ecological Society of America.
Without sea otters present, (25) nevertheless–––––––––––––, kelp forests run the danger of becoming barren stretches of coastal wasteland known as urchin barrens.
[1] What was less well-known, until recently at least, was how this relationship among sea otters, sea urchins, and kelp forests might help fight global warming. [2] The amount of carbon dioxide in the atmosphere has increased 40 percent (26) . [3] A recent study by two professors at the University of California, Santa Cruz, Chris Wilmers and James Estes, (27) suggests, that––––––––––––––– kelp forests protected by sea otters can absorb as much as twelve times the amount of carbon dioxide from the atmosphere as those where sea urchins are allowed to (28) devour–––––––– the kelp. [4] Like (29) their––––– terrestrial plant cousins, kelp removes carbon dioxide from the atmosphere, turning it into sugar fuel through photosynthesis, and releases oxygen back into the air.
[5] Scientists knew this but did not recognize (30) how large a role they played–––––––––––––––––––––––––––––– in helping kelp forests to significantly decrease the amount of carbon dioxide in the atmosphere. [6] Far from making no difference to the ecosystem, the presence of otters was found to increase the carbon storage of kelp forests by 4.4 to 8.7 megatons annually, offsetting the amount of carbon dioxide emitted by three million to six million passenger cars each year. (31)
Wilmers and Estes caution, however, that (32) having more otters––––––––––––––––––––– will not automatically solve the problem of higher levels of carbon dioxide in the air. But they suggest that the presence of otters provides a good model of how carbon can be sequestered, (33) or removed, from––––––––––––––––––– the atmosphere through the management of animal populations. If ecologists can better understand what kinds of impacts animals might have on the environment, Wilmers contends, “there might be opportunities for win-win conservation scenarios, whereby animal species are protected or enhanced, and carbon gets sequestered.”
Where is the most logical place in this paragraph to add the following sentence?
What Wilmers and Estes discovered in their study, therefore, surprised them.AAfter sentence 1BAfter sentence 3CAfter sentence 4DAfter sentence 5
In a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A current of 1 A flows through a copper wire. The number of electrons passing through any cross-section of the wire in 1.6 sec is (charge of a electron = 1.6 xx 10^(-19 c).
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. Choose the current statements
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A uniform wire of length 2.0 m and cross-sectional area 10−7m2 carries a current of 1.6 A. If there are 1028 free electrons per m in copper, the drift speed of electrons in copper is
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor.
If no potential difference is maintained between the ends of a conductor
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. The drift speed of free electrons in a conductor depends upon
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A constant potential difference is maintained between the ends of a conductor having nonuniform cross-section. Which of the following quantities will not change along the length of the conductor
View SolutionWhen an atom or an ion is missing from its nomal lattice site a lattice vacanecy (Schottky defect) is created. In stoichmeteric ionic crystals, a vacancy of one ion has to be accompanied by the vacancy of the oppositely charge ion in order to maintain electrical neutrality.
In a Frenkel defect an ion leaves its position in the lattice and occupies an interstitial void. This id the Frenkel defect commonly found along with the Schottky defects and interstitial. In pure alkali halides. Frenked defects are not found since the ions cannot get into the interstitial sites. Frenkel defects are found in silver halides because of the small size of the Ag+ ion. Unike Schottky defects, Frenkel defect do not change the density of the solids. in certain ionic solids (e.g., AgBr) both schottky and Frenkel defect occur.
The Defects idiscussed above do not disturb the stoichiometery of the crystalline material. there is large variety of non-stoichiometric inorganic solids which contains an excess or deficienty of one of the elements. Such solids showing deviations from the ideal stoichiometric composition from an important group of solids. For example in the vanadium oxide, VOx,x can be anywehere between 0.6 and 1.3 there are solids such as difficult to prepare in the soichiometric omposition thus, the ideal composition in compounds such as FeO is difficult to obtain (normally we get a compositiion of Fe(0.95)O but it may range from Fe0.93O to Fe0.96O). Non-stoichiometric behavious is most commonly found for transition metal compounds through is also known for some lathanoids and actinoids.
Zinc oxide loses oxygen reversible at high temperature and turns yellow in colour. the excess metal is accomodated interstitial, giving rise to electrons trapped in the neighbourhood, the enchanced electrical conductivity of the non-stoichiometric ZnO arises from these electrons.
Anion vacancies in alkali halides are produced by heating the alkali halid crystals in an atmosphere of the alkali metal vapour. when the metal atoms deposit on the surface they diffuse into the cystal and after ionisation the alkali metal ion occupies cationic vacancy whereas electron occupies anionic vacancy. Electrons trapped i anion vacancies are referred to as F-centers (From Farbe the German word for colouf) that gives rise to interesting colour in alkali halides. Thus, the excess of potassium i KCl makes the crystal appear violet and the excess of lithium in LiCl makes it pink.
Which of the following is most appropritate crystal to show Frenkel defect ?
View Solution
