For the second order reaction, concentration (x) of the product at time t starting with initial concentration [A]o is :
kt[Ao]21+kt[Ao]
k[Ao]21+kt
1+kt[Ao]2k+[Ao]2
None of these
The correct Answer is:A
To solve the problem regarding the concentration x of the product at time t for a second-order reaction starting with an initial concentration (A)0, we can follow these steps:
1. Understanding the Second Order Reaction:
For a second-order reaction, the rate law can be expressed as:
Rate=k(A)2
where k is the rate constant and (A) is the concentration of reactant A.
2. Using the Integrated Rate Law:
The integrated rate law for a second-order reaction is given by:
1(A)−1(A)0=kt
where (A)0 is the initial concentration and (A) is the concentration at time t.
3. Expressing Concentration at Time t:
Rearranging the integrated rate law gives:
1(A)=kt+1(A)0
Thus, we can express (A) as:
(A)=1kt+1(A)0
4. Relating Concentration of Product x:
The concentration of the product x formed at time t can be related to the change in concentration of A:
x=(A)0−(A)
Substituting the expression for (A):
x=(A)0−1kt+1(A)0
5. Finding a Common Denominator:
To simplify the expression, we can find a common denominator:
x=(A)0−1kt(A)0+1
This can be rewritten as:
x=(A)0(kt(A)0+1)−1kt(A)0+1
6. Final Expression for x:
After simplifying, we arrive at the expression:
x=(A)20ktkt(A)0+1
Final Answer:
The concentration x of the product at time t for a second-order reaction starting with initial concentration (A)0 is:
x=(A)20ktkt(A)0+1
For a second-order reaction, the rate law can be expressed as:
Rate=k(A)2
where k is the rate constant and (A) is the concentration of reactant A.
The integrated rate law for a second-order reaction is given by:
1(A)−1(A)0=kt
where (A)0 is the initial concentration and (A) is the concentration at time t.
Rearranging the integrated rate law gives:
1(A)=kt+1(A)0
Thus, we can express (A) as:
(A)=1kt+1(A)0
The concentration of the product x formed at time t can be related to the change in concentration of A:
x=(A)0−(A)
Substituting the expression for (A):
x=(A)0−1kt+1(A)0
To simplify the expression, we can find a common denominator:
x=(A)0−1kt(A)0+1
This can be rewritten as:
x=(A)0(kt(A)0+1)−1kt(A)0+1
After simplifying, we arrive at the expression:
x=(A)20ktkt(A)0+1
The concentration x of the product at time t for a second-order reaction starting with initial concentration (A)0 is:
x=(A)20ktkt(A)0+1
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-2 ( Numerical Value Type for JEE Main )
15 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - JEE Main (Archive)
56 Videos
- CHEMICAL KINETICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL KINETICS EXERCISE - Level-1
75 Videos
- CHEMICAL EQUILIBRIUMBOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - IN-CHAPTER EXERCISE - G
10 Videos
- CHEMICAL THERMODYNAMICS BOOK - VMC MODULES ENGLISHCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - IN - CHAPTER EXERCISE - L
10 Videos
Similar Questions
Knowledge Check
In a first order reaction, The concentration of reactant is reduced to 1/8th of the initial concentration in 75 minutea at 298 K. What is the half period of the reaction in minutes?
A50 minB15 minC30 minD25 minThe reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
Athe same as the initial valueBthree times the initial valueCdouble the initial valueDhalf the initial value.The reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
Athe same as the initial valueBthree times the initial valueCdouble the initial valueDhalf the initial value.
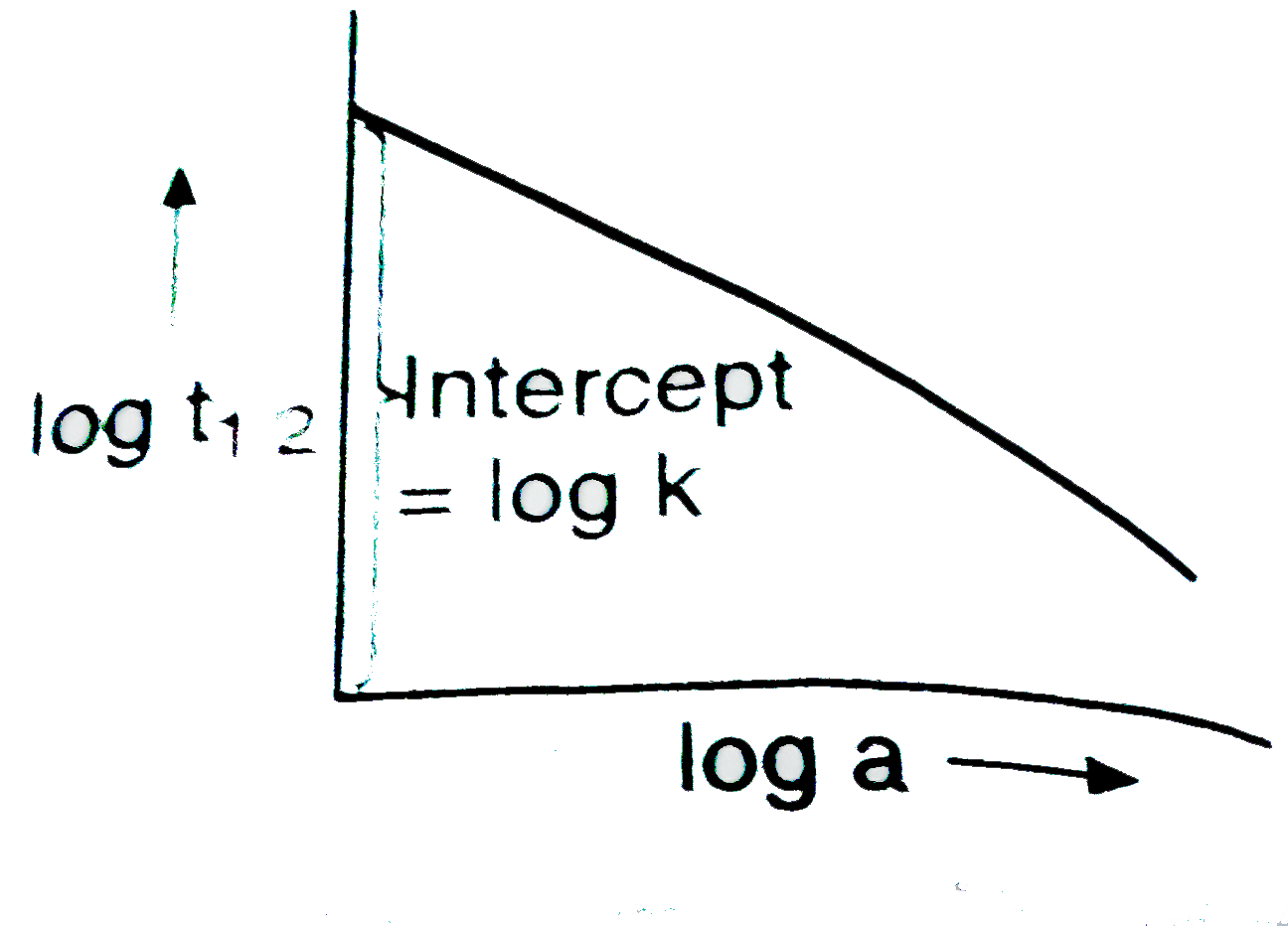
For a second order reaction, 2A→ Products, a plot of log t1/2 vs log a (where a is initial concentration) will give an intercept equal to which one of the following?
View SolutionFor a certain first order reaction, the concentration of the reactant decreases to nine-tenth of its initial value in ten minutes. Concentration of the reactant after 30 minutes from start will be :
View SolutionFor a zero order reaction, the half-life periof is independent of the initial concentration.
View SolutionHalf life (t1) of the first order reaction and half life (t2) of the 2nd order reaction are equal. If initial concentration of reactants in both reaction are same then ratio of the initial rate of the reaction
View SolutionThe reaction between X and Y is first order with respect to X and second order with respect to Y. If the concentration of X is halved and the concentration of Y is doubled, the rate of reaction will be
View Solution
