The dimensions of 12ε0E2, where ε0 is permittivity of free space and E is electric field, are
[M−1L2T−2]
[ML−1T−2]
[ML2T−1]
[MLT−1]
The correct Answer is:B
Step by step video & image solution for The dimensions of (1)/(2)epsilon_(0)E^(2), where epsilon_(0) is permittivity of free space and E is electric field, are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Illustration24videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - SOLVED EXAMPLES20videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Efficient50videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE56videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)4videos
WAVE MOTION
Similar Questions
The dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimensions of 12ε0E2(ε0= permittivity of free space, E= electric field) is
View SolutionThe dimensions of (μ0ε0)−1/2 are
View SolutionThe dimensions of ε0μ0 are
View SolutionA wire of length L= 20 cm is bent into a semicircular arc and the two equal halves of the arc are uniformly charged with charges +Q and −Q as shown in the figure. The magnitude of the charge on each half is |Q|=103ε0, where ε0 is the permittivity of free the space. The net electric field at the center O is
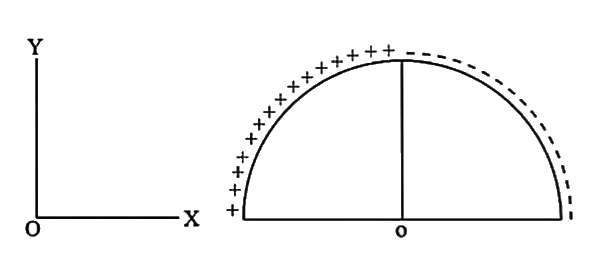 View Solution
View SolutionThe dimensions of 12∈0E2 (∈0: permittivity of free space, E: electric field) is-
View SolutionThe quantity X=ε0LVt where ε0 is the permittivity of free space, L is length, V is the potential difference and t is time. The dimensions of X are the same as that of
View SolutionA quantity X is given by ε0LΔVΔt, where ε0 is the permittivity of free space L is a length ΔV is a potnetial difference and Δ is a time internval. The dimensional forumla to X is the same as that of
View Solutionε0E2 has the dimensions of
(ε0= permittivity of free space, E= electric field)
Here k= Boltzmann consant
T= absolute temperature
R= universal gas constant.View Solution

