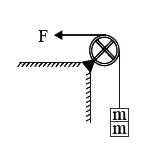
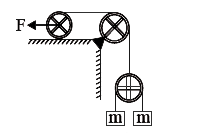
A man thinks about 4 arrangements as shown to raise two small bricks each having mass m. Which of the arrangement would take minimum time ?
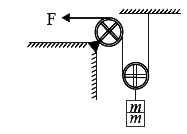

The correct Answer is:1
To determine which arrangement takes the minimum time to raise two small bricks, each with mass m, we need to analyze the acceleration produced in each arrangement. The key principle here is that to minimize time, we need to maximize acceleration, which in turn requires maximizing the net force acting on the system.
1. Understanding the Problem:
We have four different arrangements to lift two bricks, and we need to find out which one allows for the maximum acceleration, thus minimizing the time taken to lift them.
2. Applying Newton's Second Law:
According to Newton's second law, the acceleration a of an object is given by the formula:
a=Fnetm
where Fnet is the net force acting on the object and m is its mass.
3. Analyzing Each Arrangement:
- Arrangement A: The force F is applied directly to the system, resulting in a total force of 2F acting on the two bricks. Thus, the acceleration is:
aA=2F2m=Fm
- Arrangement B: Here, a force is applied to a wheel, and due to friction, the effective tension T is less than F. Therefore, the acceleration is:
aB<Fm
- Arrangement C: The force F is applied to the string, resulting in a tension T=F. The acceleration for this arrangement is:
aC=F2m
(since the force is distributed between two masses).
- Arrangement D: Similar to arrangement C, the force is divided, leading to a lower effective tension. Thus, the acceleration is:
aD<F2m
4. Comparing Accelerations:
From our calculations:
- aA=Fm
- aB<Fm
- aC=F2m
- aD<F2m
It is clear that aA is the largest acceleration.
5. Conclusion:
Since arrangement A provides the maximum acceleration, it will take the minimum time to raise the two bricks. Therefore, the correct answer is:
Arrangement A takes the minimum time.
We have four different arrangements to lift two bricks, and we need to find out which one allows for the maximum acceleration, thus minimizing the time taken to lift them.
According to Newton's second law, the acceleration a of an object is given by the formula:
a=Fnetm
where Fnet is the net force acting on the object and m is its mass.
- Arrangement A: The force F is applied directly to the system, resulting in a total force of 2F acting on the two bricks. Thus, the acceleration is:
aA=2F2m=Fm
aB<Fm
aC=F2m
(since the force is distributed between two masses).
aD<F2m
From our calculations:
- aA=Fm
- aB<Fm
- aC=F2m
- aD<F2m
Since arrangement A provides the maximum acceleration, it will take the minimum time to raise the two bricks. Therefore, the correct answer is:
Arrangement A takes the minimum time.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is :

View SolutionThe arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass m, on which two light theads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

View Solution
Knowledge Check
Four particles of masses m, 2m, 3m and 4m are arranged at the corners of a parallelogram with each side equal to a and one of the angle between two adjacent sides is 60∘. The parallelogram lies in the x-y plane with mass m at the origin and 4 m on the x-axis. The centre of mass of the arrangement will be located at
A(√32a,0.95a)B(0.95a,√34a)C(3a4,a2)D(a2,3a4)
Two point masses, m each carrying charges −q and +q are attached to the ends of a massless rigid non - conducting wire of length L. When this arrangement is placed in a uniform electric field, then it deflects through an angle θ. The minimum time needed by the rod to align itself along the field is
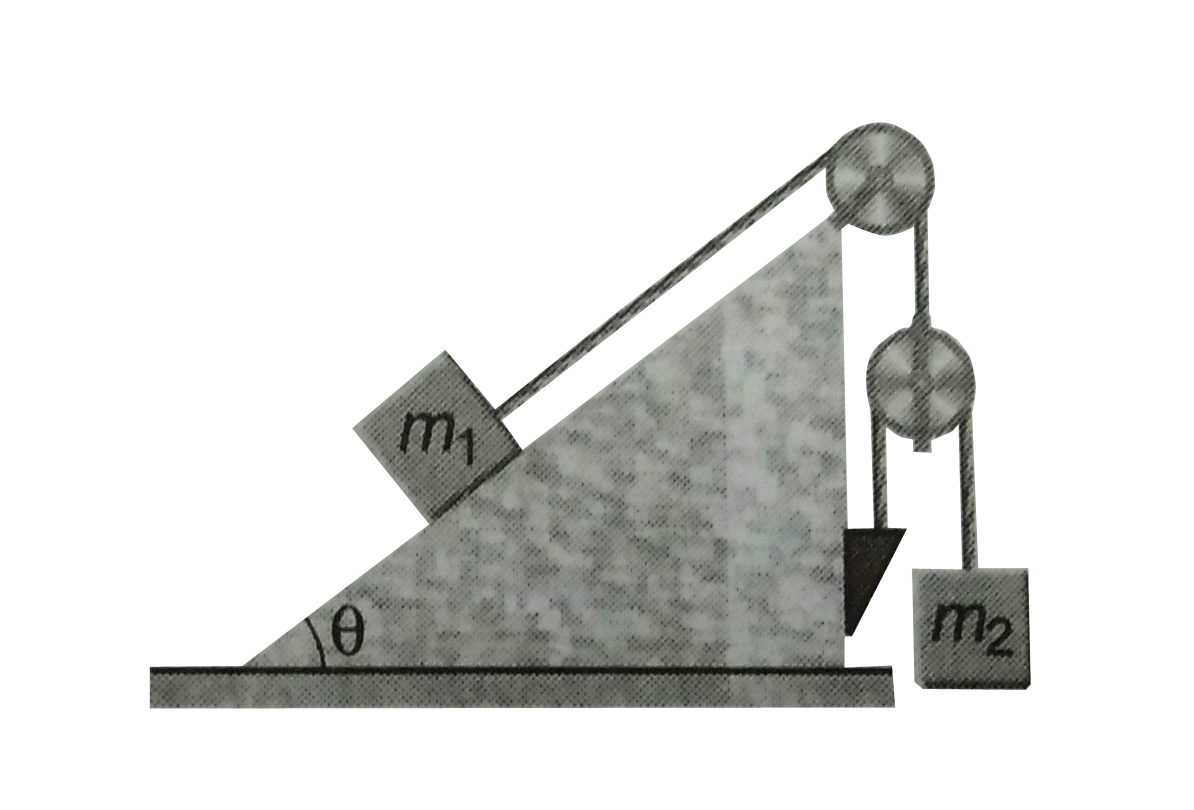
View SolutionFind the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are assumed to be negligible.
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionFor the arrangement shown in the switch is closed at t =0. The time after which the current becomes 2.5μAS is given by (take in 2 =0.69)
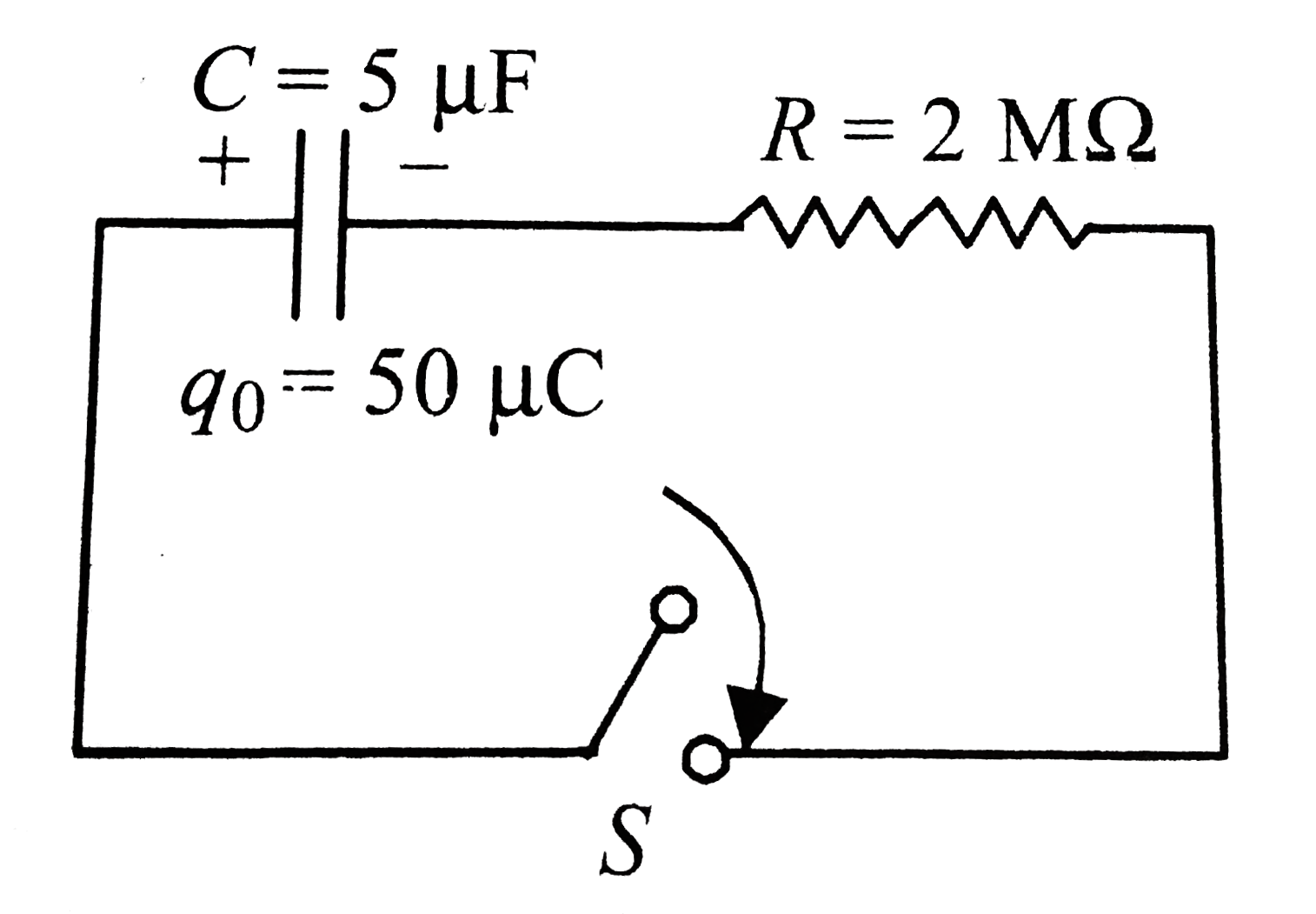
View SolutionIn the arrangement shown in figure, the rod of mass mheld by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

View SolutionIn the arrangements shown in the figure masses of each ball is 1kg and mass of trolley is 4kg. In the figure, shell of mass 1kg moving horizontally with velocity v=6ms−1 collides with the ball and get stuck to it then its maximum deflection of the thread (length 1.5m) with vertical

View SolutionSeven homogeneous bricks, each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L10. Find the x-coordinate of the centre of mass relative to the origin shown.

View Solution
