An engine is working at a constant power draws a load of mass m against a resistance r. Find maximum speed of load and time taken to attain half this speed.
(a)
(b)
(c)
(d)
The correct Answer is:A
To solve the problem of an engine working at a constant power that draws a load of mass m against a resistance r, we need to find the maximum speed of the load and the time taken to attain half of this speed.
1. Understanding Power and Force Relationship:
The power P of the engine is given by the formula:
P=F⋅v
where F is the force exerted by the engine and v is the velocity of the load. In this case, the force F is equal to the resistance r that the engine has to overcome.
2. Setting Up the Equation:
Since the engine is working against the resistance, we can write:
P=r⋅v
Rearranging this gives us:
v=Pr
This equation shows that the maximum speed vmax of the load is directly proportional to the power and inversely proportional to the resistance.
3. Finding Maximum Speed:
From the equation derived, we find the maximum speed:
vmax=Pr
4. Finding Time to Attain Half the Speed:
We need to find the time taken to reach half of the maximum speed, which is:
v=vmax2=P2r
5. Using the Relationship Between Force, Mass, and Acceleration:
The force can also be expressed using Newton's second law:
F=m⋅a
where a is the acceleration. Since a=dvdt, we can write:
r=m⋅dvdt
6. Rearranging and Integrating:
Rearranging gives:
m⋅dv=r⋅dt
Integrating both sides, we set the limits for v from 0 to P2r and for t from 0 to t:
∫P2r0mdv=∫t0rdt
This results in:
m⋅(P2r−0)=r⋅t
Simplifying gives:
mP2r=rt
Therefore, solving for t:
t=mP2r2
Final Answers:
- Maximum Speed: vmax=Pr
- Time to attain half the speed: t=mP2r2
The power P of the engine is given by the formula:
P=F⋅v
where F is the force exerted by the engine and v is the velocity of the load. In this case, the force F is equal to the resistance r that the engine has to overcome.
Since the engine is working against the resistance, we can write:
P=r⋅v
Rearranging this gives us:
v=Pr
This equation shows that the maximum speed vmax of the load is directly proportional to the power and inversely proportional to the resistance.
From the equation derived, we find the maximum speed:
vmax=Pr
We need to find the time taken to reach half of the maximum speed, which is:
v=vmax2=P2r
The force can also be expressed using Newton's second law:
F=m⋅a
where a is the acceleration. Since a=dvdt, we can write:
r=m⋅dvdt
Rearranging gives:
m⋅dv=r⋅dt
Integrating both sides, we set the limits for v from 0 to P2r and for t from 0 to t:
∫P2r0mdv=∫t0rdt
This results in:
m⋅(P2r−0)=r⋅t
Simplifying gives:
mP2r=rt
Therefore, solving for t:
t=mP2r2
- Maximum Speed: vmax=Pr
- Time to attain half the speed: t=mP2r2
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - ENABLE
50 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A car of mass m has an engine which can deliver constant power P.the maximum speed that the car can attain in t seconds in
View SolutionA bus of mass 1000 kg has an engine which produces a constant power of 50 kW. If the resistance to motion, assumed constant is 1000 N. The maximum speed at which the bus can travel on level road and the acceleration when it is travelling at 25 m/s, will respectively be -
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
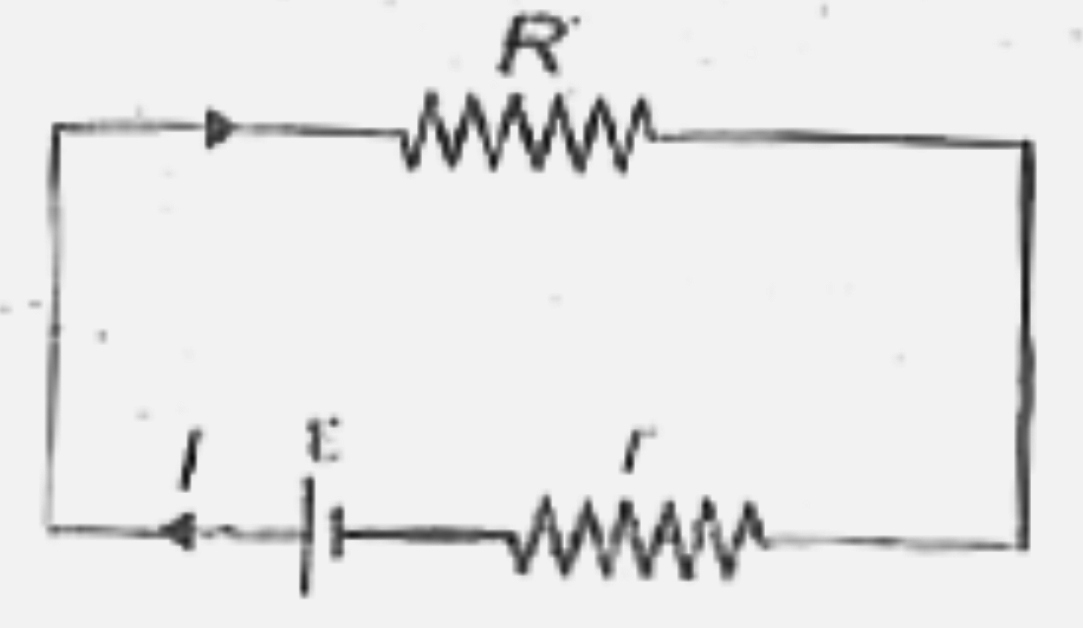
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA train has a constant speed of 40 ms−1 on a level road against resistive force of magnitude 3×104N. Find the power of the engine.
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r. Find magnitude of average force on it in half revolution.
View SolutionEngine of car of mass m supplies a constant power P. Starting from rest at an instant of time, then
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionA cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
View SolutionAn alternating current generator has an internal resistance Rg and an internal reactance Xg. It is used to supply power to a passive load consisting of a resistance Rg and a reactance XL. For maximum power to be delivered from the generator to the load, the value of XL is equal to
View Solution
