The magnetic field midway between two parallel current carrying wires, carrying currents I and 2i in same direction is B. If the current in the wire with current I is switched off, the magnetic field will become
B/3
2B
B/2
B/4
The correct Answer is:B
To solve the problem, we need to analyze the magnetic fields produced by two parallel current-carrying wires and how the magnetic field changes when one of the currents is turned off.
1. Understanding the Setup:
- We have two parallel wires. Wire 1 carries a current I and Wire 2 carries a current 2I. Both currents are in the same direction.
- We need to find the magnetic field at the midpoint between these two wires.
2. Magnetic Field Due to a Long Straight Current-Carrying Wire:
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- For Wire 1 (current I):
B1=μ0I2πr
- For Wire 2 (current 2I):
B2=μ0(2I)2πr=2μ0I2πr=μ0Iπr
3. Direction of the Magnetic Fields:
- Using the right-hand rule, the magnetic field due to Wire 1 (B1) at the midpoint will be directed into the plane of the paper.
- The magnetic field due to Wire 2 (B2) will be directed out of the plane of the paper.
4. Net Magnetic Field at the Midpoint:
- Since B1 is into the plane and B2 is out of the plane, the net magnetic field B at the midpoint is:
B=B2−B1=μ0Iπr−μ0I2πr
- Simplifying this:
B=μ0Iπr−μ0I2πr=2μ0I2πr−μ0I2πr=μ0I2πr=B
5. Switching Off the Current in Wire 1:
- When the current I in Wire 1 is switched off, the magnetic field at the midpoint will only be due to Wire 2:
B′=B2=μ0(2I)2πr=2μ0I2πr=2B
6. Conclusion:
- Therefore, when the current in Wire 1 is switched off, the magnetic field at the midpoint becomes:
B′=2B
Final Answer:
The magnetic field will become 2B.
---
- We have two parallel wires. Wire 1 carries a current I and Wire 2 carries a current 2I. Both currents are in the same direction.
- We need to find the magnetic field at the midpoint between these two wires.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- For Wire 1 (current I):
B1=μ0I2πr
- For Wire 2 (current 2I):
B2=μ0(2I)2πr=2μ0I2πr=μ0Iπr
- Using the right-hand rule, the magnetic field due to Wire 1 (B1) at the midpoint will be directed into the plane of the paper.
- The magnetic field due to Wire 2 (B2) will be directed out of the plane of the paper.
- Since B1 is into the plane and B2 is out of the plane, the net magnetic field B at the midpoint is:
B=B2−B1=μ0Iπr−μ0I2πr
- Simplifying this:
B=μ0Iπr−μ0I2πr=2μ0I2πr−μ0I2πr=μ0I2πr=B
- When the current I in Wire 1 is switched off, the magnetic field at the midpoint will only be due to Wire 2:
B′=B2=μ0(2I)2πr=2μ0I2πr=2B
- Therefore, when the current in Wire 1 is switched off, the magnetic field at the midpoint becomes:
B′=2B
The magnetic field will become 2B.
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - ENABLE
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
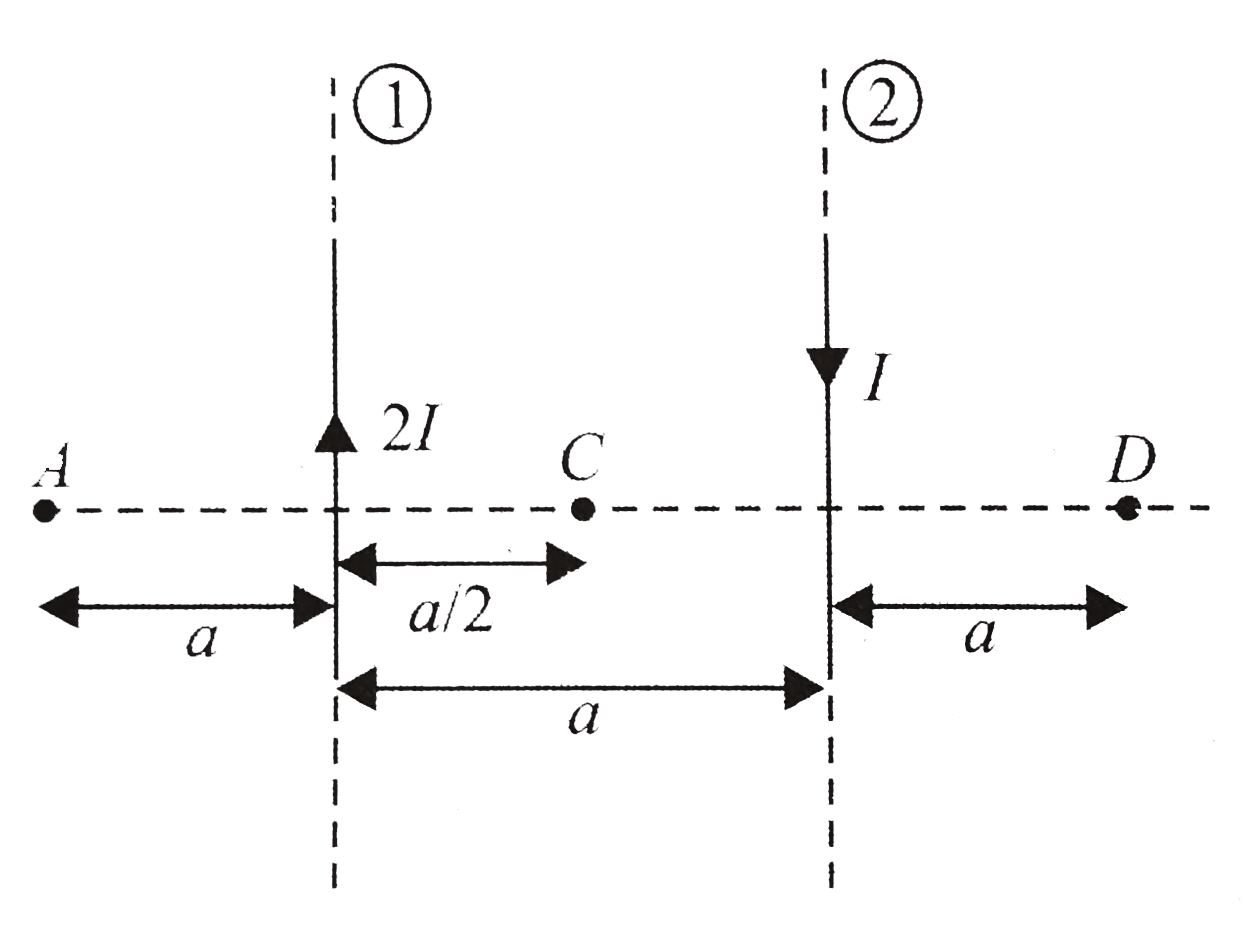
Find magnetic field at C by the system of current carrying wire.

View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionTwo parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionMagnetic field at a distance a from long current carrying wire is proportional to
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is

View SolutionA wire is parallel to a square coil . The coil and wire carry currents in the directions Shown . Then, at any point A within the coil the magnetic field will be -

View SolutionA current carrying wire is placed along east and west in a magnetic field directed north wards. If the current in the wire is directed east wards, the direction of force on the wire is
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View Solution
