The magnetic induction at the centre of a solenoid is . If the length of the solenoid is reduced to half and the same wire is would in two layers the new magnetic induction is
B
2B
4B
The correct Answer is:B
To solve the problem, we need to analyze the changes in the solenoid's dimensions and how they affect the magnetic induction (B) at its center.
1. Understand the initial conditions:
- The magnetic induction at the center of the solenoid is given as B.
- The formula for the magnetic induction at the center of a solenoid is:
B=μ0nI2
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current through the wire.
2. Initial length and turns:
- Let the initial length of the solenoid be L and the number of turns be N.
- Therefore, the number of turns per unit length n is:
n=NL
3. Reducing the length:
- The length of the solenoid is reduced to half, so the new length L′ is:
L′=L2
4. Winding the same wire in two layers:
- Since the same wire is used, the total number of turns N remains the same.
- However, when the solenoid is wound in two layers, the effective number of turns per unit length n′ doubles because the same number of turns is now spread over half the length:
n′=NL′=NL/2=2NL=2n
5. New magnetic induction:
- Substitute n′ into the formula for magnetic induction:
B′=μ0n′I2=μ0(2n)I2=μ0nI=2B
6. Final calculation:
- Since we have reduced the length and doubled the number of turns per unit length, the new magnetic induction B′ becomes:
B′=4B
Conclusion:
The new magnetic induction at the center of the solenoid after reducing its length to half and winding the same wire in two layers is:
B′=4B
- The magnetic induction at the center of the solenoid is given as B.
- The formula for the magnetic induction at the center of a solenoid is:
B=μ0nI2
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current through the wire.
- Let the initial length of the solenoid be L and the number of turns be N.
- Therefore, the number of turns per unit length n is:
n=NL
- The length of the solenoid is reduced to half, so the new length L′ is:
L′=L2
- Since the same wire is used, the total number of turns N remains the same.
- However, when the solenoid is wound in two layers, the effective number of turns per unit length n′ doubles because the same number of turns is now spread over half the length:
n′=NL′=NL/2=2NL=2n
- Substitute n′ into the formula for magnetic induction:
B′=μ0n′I2=μ0(2n)I2=μ0nI=2B
- Since we have reduced the length and doubled the number of turns per unit length, the new magnetic induction B′ becomes:
B′=4B
The new magnetic induction at the center of the solenoid after reducing its length to half and winding the same wire in two layers is:
B′=4B
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - ENABLE
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
The magnetic induction at centre O Fig.
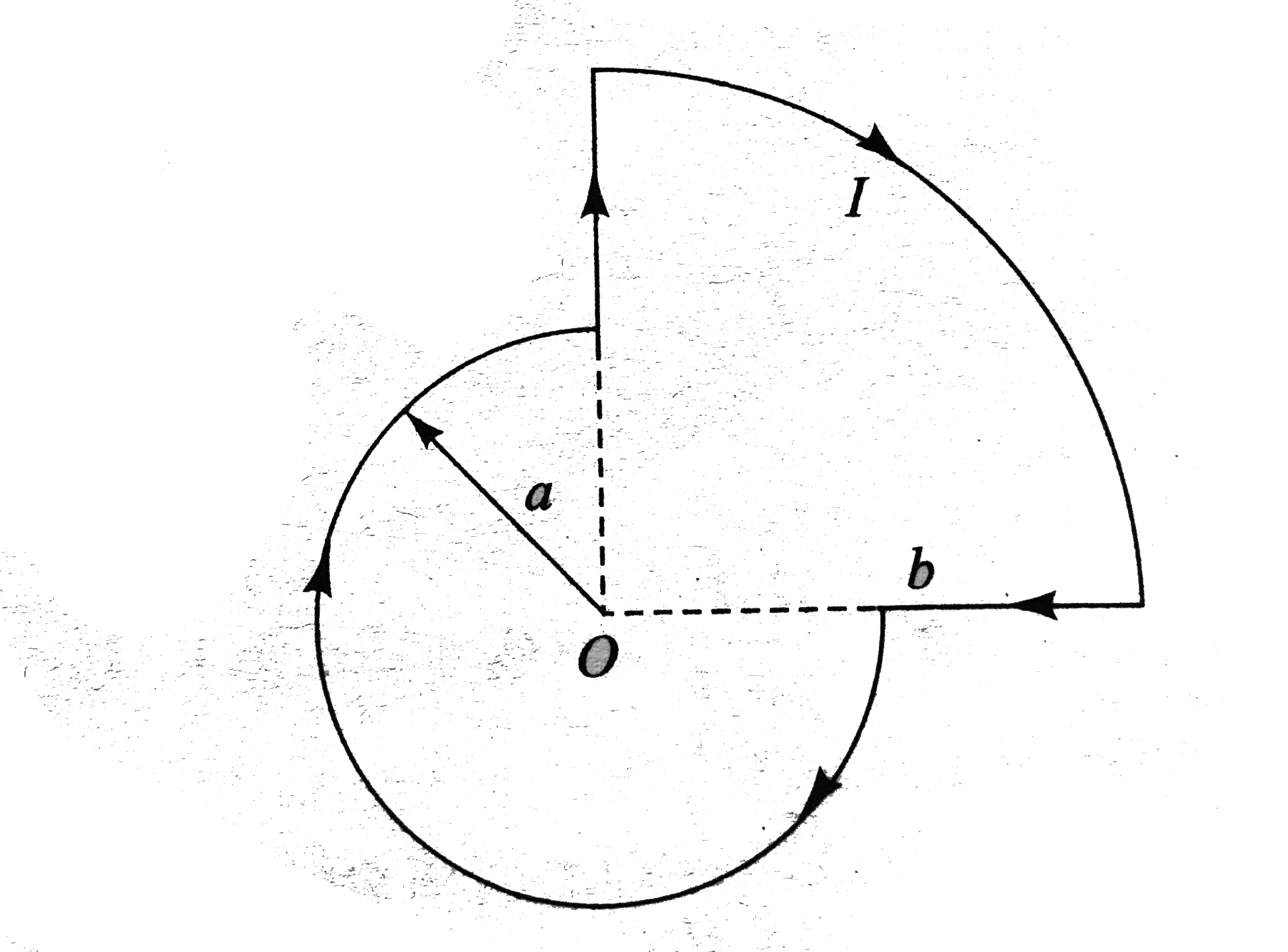
View SolutionThe magnetic induction at centre O in the following figure will be

View SolutionWhen a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to some current flowing is B1 If the same wire is turned into three loops to make a circular coil, the magnetic induction at the center of this coil for the same current will be
View SolutionUnit of magnetic induction field B is
View SolutionThe dimensional formula of magnetic induction B is
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is

View SolutionA solenoid have self inductance 2H. If length of the solenoid is double having turn density and area constant then new self inductance is :-
View SolutionA tightly-wound, long solenoid having 50 turns cm−1, carris a current of 4.00A. Find the magnetic intensity H and the magnetic field B at the centre of the solenoid. What will be the values of these quantities if an iron core is inserted in the solenoid and the magnetization I in the core is 4.00×106Am−1 ?
View SolutionA tightly- wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surgace current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
View SolutionThe length of a solenoid is 0.1m and its diameter is very small . A wire is wound over in two layers. The number of turns in the inner layer is 50 and that on the outer layer is 40. The strength of current flowing in two layers in the same direction is 3 ampere. The magnetic induction in the middle of the solenoid will be
View Solution
