Force per unit length acting at one end of each of the two long parallel wires, carrying current I each, kept distance r apart is
(a)μ04πi2r
(b)μ04π2i2r
(c)μ04π(2i)2r
(d)μ04πi24r
The correct Answer is:B
To find the force per unit length acting at one end of each of the two long parallel wires carrying current I and separated by a distance r, we can follow these steps:
1. Understanding the Setup:
- We have two long parallel wires, each carrying the same current I.
- The distance between the two wires is r.
2. Direction of Forces:
- If the currents in both wires are in the same direction, they will attract each other.
- If the currents are in opposite directions, they will repel each other.
3. Magnetic Field Due to a Current-Carrying Wire:
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
4. Force on a Current-Carrying Wire in a Magnetic Field:
- The force F experienced by a wire of length L carrying current I in a magnetic field B is given by:
F=I⋅L⋅B
5. Calculating the Force per Unit Length:
- For wire 1, the magnetic field at its location due to wire 2 is:
B=μ0I2πr
- The force on wire 1 due to the magnetic field created by wire 2 is:
F1=I⋅L⋅B=I⋅L⋅μ0I2πr
- The force per unit length FL is:
F1L=μ0I22πr
6. Final Expression:
- Since both wires experience the same force per unit length, the final expression for the force per unit length acting at one end of each wire is:
FL=μ0I22πr
Final Answer:
The force per unit length acting at one end of each of the two long parallel wires is given by:
FL=μ0I22πr
- We have two long parallel wires, each carrying the same current I.
- The distance between the two wires is r.
- If the currents in both wires are in the same direction, they will attract each other.
- If the currents are in opposite directions, they will repel each other.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
where μ0 is the permeability of free space.
- The force F experienced by a wire of length L carrying current I in a magnetic field B is given by:
F=I⋅L⋅B
- For wire 1, the magnetic field at its location due to wire 2 is:
B=μ0I2πr
- The force on wire 1 due to the magnetic field created by wire 2 is:
F1=I⋅L⋅B=I⋅L⋅μ0I2πr
- The force per unit length FL is:
F1L=μ0I22πr
- Since both wires experience the same force per unit length, the final expression for the force per unit length acting at one end of each wire is:
FL=μ0I22πr
The force per unit length acting at one end of each of the two long parallel wires is given by:
FL=μ0I22πr
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - ENABLE
50 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
Calculate the force per unit length on a long straight wire carrying current 4A due to parallel wire carrying current 6A current. Distance between the wires =3cm.
View SolutionCalculate the self inductance per unit length of a current loop formed by joining the ends of two long parallel wires of radius r separated by a distance d between their axes, neglecting the end effects and magnetic flux within the wires.
View SolutionCalculate force per unit length acting on the wire B due to the current flowing in the wire A. (see figure below)
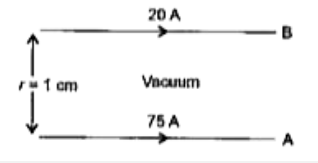
View SolutionDerive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionThe force between two parallel current carrying wires is independent of
View SolutionFind the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
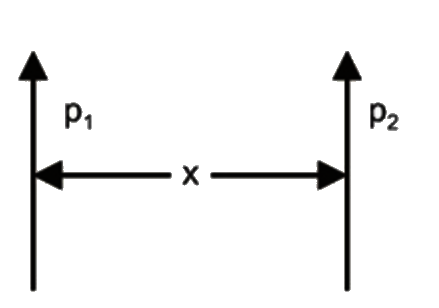
View SolutionWrite an expression for force per unit length between two long current carrying wires, kept parallel to each other, in vacuum and hence define an ampere, the SI unit of current
View SolutionTwo long straight parallel wires, carrying (adjustable) currents I1 and I2 are kept at a distance d apart. If the force F between the two wires is taken as positive when the wire repel each other and negative when the wires attract each other, the graph showing the dependence of F, on the product I1I2 would be:
View SolutionHow much force per unit length acts on a long current carrying conductor X due to a current flowing through another similar conductor Y, kept parallel to it in vacuum ? Use this equation to define an ampere, the fundamental unit of current.
View Solution
