A sinusoidal ac current flows through a resistor of resistance R . If the peak current is , then the power dissipated is
(a)
(b)
(c)
(d)
The correct Answer is:B
To solve the problem of finding the power dissipated in a resistor when a sinusoidal AC current flows through it, we can follow these steps:
1. Understand the Given Information:
- We have a sinusoidal AC current flowing through a resistor of resistance R.
- The peak current is given as Ip.
2. Determine the RMS Current:
- The root mean square (RMS) value of a sinusoidal current is related to its peak value by the formula:
Irms=Ip√2
- This formula indicates that the RMS current is the peak current divided by the square root of 2.
3. Use the Power Formula:
- The power dissipated in a resistor due to an electric current is given by the formula:
P=I2R
- Since we are dealing with an AC current, we will use the RMS value of the current in this formula.
4. Substitute the RMS Current into the Power Formula:
- Replace I in the power formula with Irms:
P=(Irms)2R
- Substituting the expression for Irms:
P=(Ip√2)2R
5. Simplify the Expression:
- Simplifying the equation gives:
P=I2p2R
6. Final Result:
- The power dissipated in the resistor is:
P=12I2pR
Conclusion:
The power dissipated in the resistor when a sinusoidal AC current flows through it is 12I2pR.
- We have a sinusoidal AC current flowing through a resistor of resistance R.
- The peak current is given as Ip.
- The root mean square (RMS) value of a sinusoidal current is related to its peak value by the formula:
Irms=Ip√2
- This formula indicates that the RMS current is the peak current divided by the square root of 2.
- The power dissipated in a resistor due to an electric current is given by the formula:
P=I2R
- Since we are dealing with an AC current, we will use the RMS value of the current in this formula.
- Replace I in the power formula with Irms:
P=(Irms)2R
- Substituting the expression for Irms:
P=(Ip√2)2R
- Simplifying the equation gives:
P=I2p2R
- The power dissipated in the resistor is:
P=12I2pR
The power dissipated in the resistor when a sinusoidal AC current flows through it is 12I2pR.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - EFFICIENT49videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G10videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
When a current I flows through a resistance R for time t, the electrical energy spent is :
AIRtBI2RtCIR2tDI2R/t
In an AC circuit with voltage V and current I, the power dissipated is
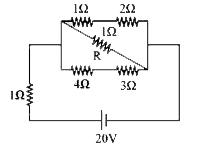
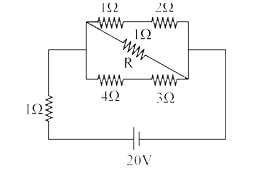
View SolutionCalculate the current flows through resistance 2Ω.
 View Solution
View SolutionA variable current flows through a 1Ω resistor for 2 s. Time dependence of the current is shown in the graph.
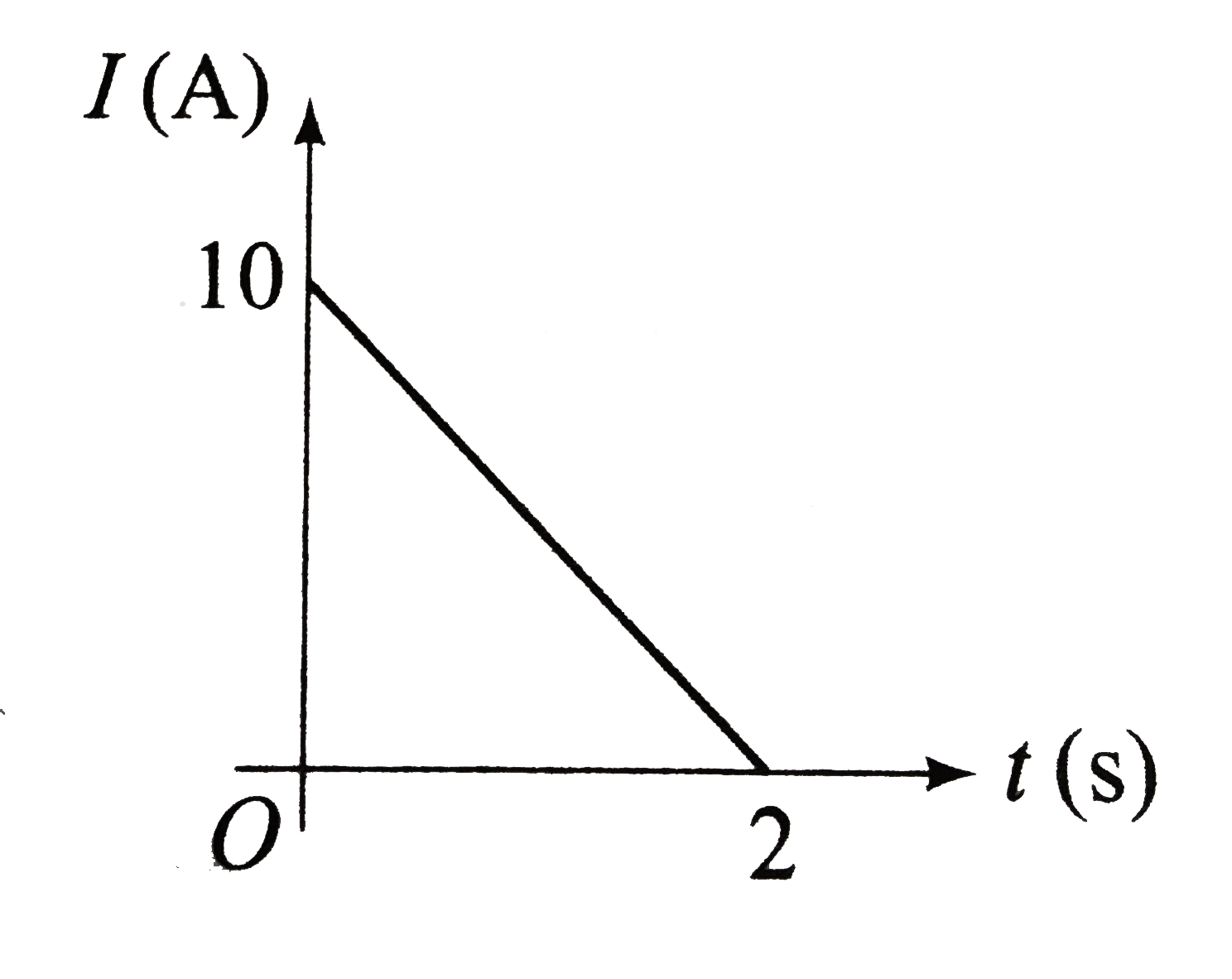 View Solution
View SolutionA sinusoidal alternating current of peak value (I0) passes through a heater of resistance R. What is the mean power output of the heater?
View SolutionThe values of current (I) flowng through a given resistor of resistance (R ), for the corresponding values of potential difference (V) across the resistor are as given below :

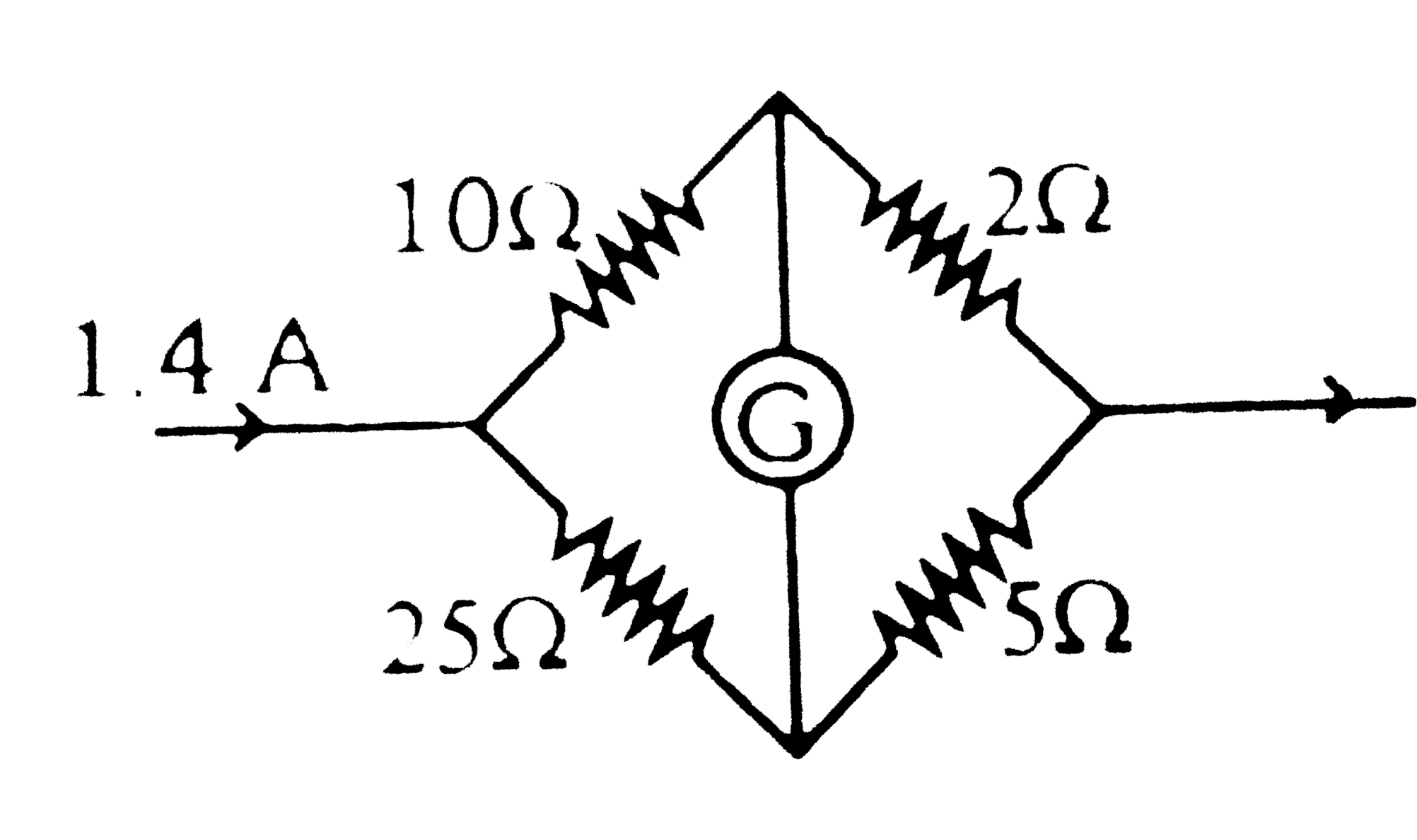
Plot a graph between current (I) and potential difference (V) and determine the resistance (R ) of the resistor.View SolutionIn the circuit, the current flowing through 10Ω resistance is
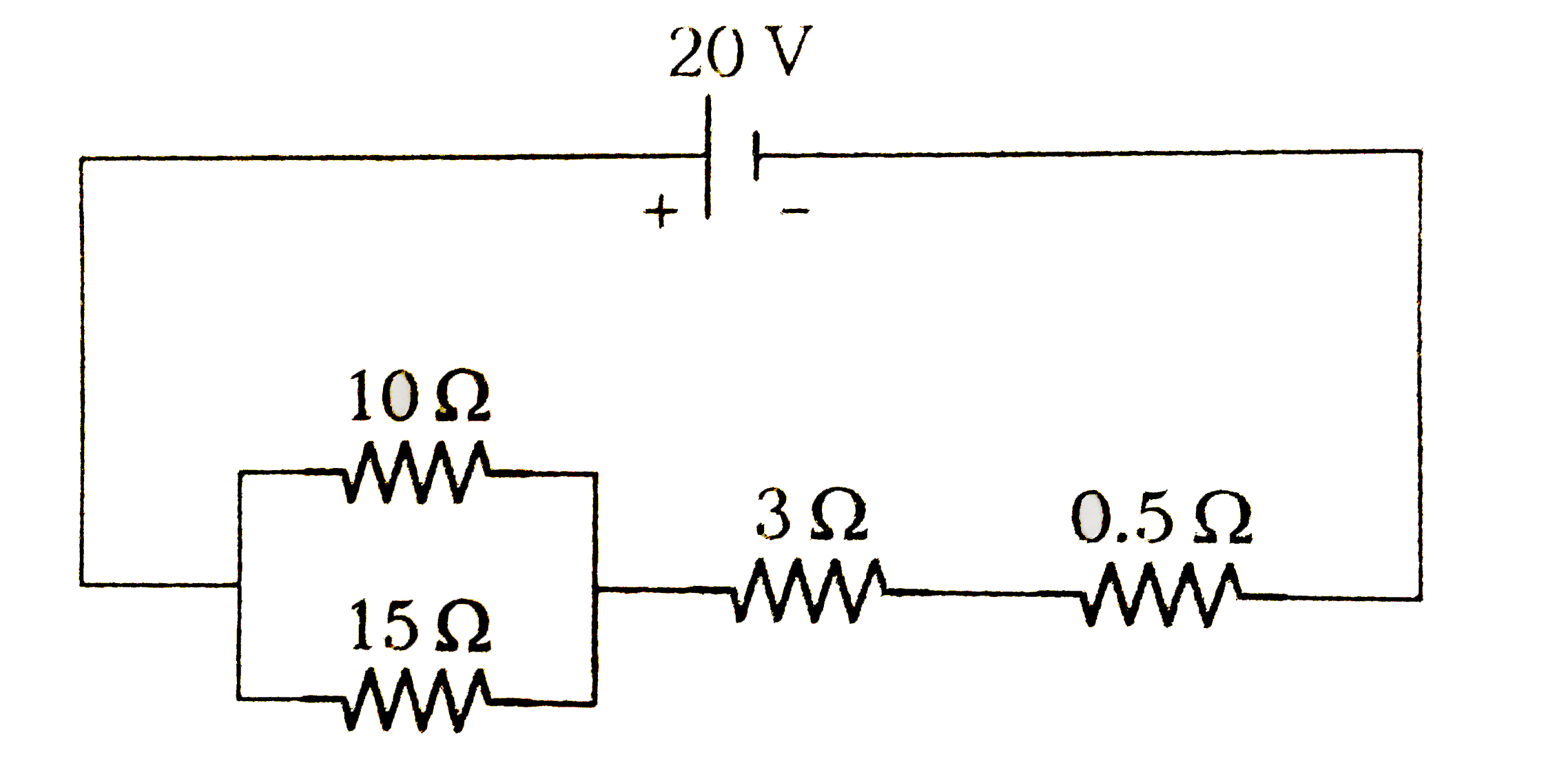 View Solution
View SolutionIf the current I through a resistor is increased by 100% (assume that temperature remains unchanged), the increase in power dissipated will be :
View Solution