The Brewster angle for the glass air interface is if a ray of light going from air to glass strikes at an angle of incidence then the angle of refraction is
(a)
(b)
(c)
(d)
The correct Answer is:B
To find the angle of refraction when a ray of light strikes the glass-air interface at an angle of incidence of 45∘, we can use Snell's Law and the information about the Brewster angle.
1. Identify the Given Information:
- Brewster angle (θB) = 54.74∘
- Angle of incidence (I) = 45∘
2. Calculate the Refractive Index:
- The refractive index (μ) can be calculated using the Brewster angle:
μ=tan(θB)
- Substitute θB:
μ=tan(54.74∘)
- Using a calculator:
μ≈1.5
3. Apply Snell's Law:
- Snell's Law states:
μ1sin(I)=μ2sin(R)
- Here, μ1=1 (for air), μ2=1.5 (for glass), I=45∘, and R is the angle of refraction we need to find.
- Substitute the known values:
1⋅sin(45∘)=1.5⋅sin(R)
4. Calculate sin(45∘):
- We know that:
sin(45∘)=1√2≈0.707
- Substitute this into the equation:
0.707=1.5⋅sin(R)
5. Solve for sin(R):
- Rearranging gives:
sin(R)=0.7071.5≈0.471
6. Find the Angle of Refraction R:
- Now, we need to find R such that:
R=arcsin(0.471)
- Using a calculator:
R≈28.1∘
Final Answer:
The angle of refraction R is approximately 28.1∘.
- Brewster angle (θB) = 54.74∘
- Angle of incidence (I) = 45∘
- The refractive index (μ) can be calculated using the Brewster angle:
μ=tan(θB)
- Substitute θB:
μ=tan(54.74∘)
- Using a calculator:
μ≈1.5
- Snell's Law states:
μ1sin(I)=μ2sin(R)
- Here, μ1=1 (for air), μ2=1.5 (for glass), I=45∘, and R is the angle of refraction we need to find.
- Substitute the known values:
1⋅sin(45∘)=1.5⋅sin(R)
- We know that:
sin(45∘)=1√2≈0.707
- Substitute this into the equation:
0.707=1.5⋅sin(R)
- Rearranging gives:
sin(R)=0.7071.5≈0.471
- Now, we need to find R such that:
R=arcsin(0.471)
- Using a calculator:
R≈28.1∘
The angle of refraction R is approximately 28.1∘.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - EFFICIENT49videos
RAY OPTICS AND WAVE OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J10videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS25videos
REVISION TEST-15 JEE - 2020
Similar Questions
Knowledge Check
- Question 1 - Select One
The critical angle for glass-air interface is :
A24∘B48∘C42∘D45∘
Light falls from glass (μ=1.5) to air. Find the angle of incidence for which the angle of deviation is 90∘.
View SolutionIf the polarising angle for air glass interface is 56.3∘, what is the angle of refraction in glass ?
View SolutionA ray of light is incident perpendicularly on a glass slab. The angle of incidence is 900.
View SolutionCritical angle of light passing from glass to air is least for
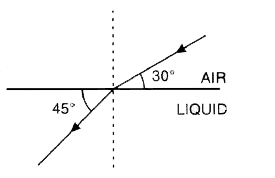
View SolutionThe diagram alongside shows the refraction of a ray of light from air to a liquid.
(a) Write the values of (i) angle of incidence, and (ii) angle of refraction.
(b) Use snell's law to find the refractive index of liquid with respect to air.
 View Solution
View SolutionThe polarizing angle of glass is 57∘ . A ray of light which is incident at this light which is incident at this angle will have an angle of refraction as
View SolutionThe critical angle between a certain transparent medium and air is ϕ. A ray of light travelling through air enters the medium at an angle of incidence equal to its Brewster angle θ. Therefore, the angle of refraction is
View Solution

