A cubic crystal possesses in all ........... planes of symmetry:
9
13
1
23
The correct Answer is:A
To determine the total number of planes of symmetry in a cubic crystal, we can follow these steps:
1. Understand the Concept of Plane of Symmetry:
- A plane of symmetry is an imaginary plane that divides a crystal into two equal halves, where one half is the mirror image of the other.
2. Identify the Structure of a Cube:
- Visualize the cubic crystal structure. A cube has three axes: the x-axis, y-axis, and z-axis.
3. Determine Rectangular Planes of Symmetry:
- A cube has three rectangular planes of symmetry, which are aligned with the axes:
- One plane parallel to the yz-plane (dividing the cube into left and right halves).
- One plane parallel to the xz-plane (dividing the cube into front and back halves).
- One plane parallel to the xy-plane (dividing the cube into top and bottom halves).
4. Determine Diagonal Planes of Symmetry:
- A cube also has six diagonal planes of symmetry. These planes cut through the cube diagonally:
- Each diagonal plane connects opposite edges of the cube.
- There are two diagonal planes for each pair of opposite faces (front-back, left-right, top-bottom).
5. Calculate Total Planes of Symmetry:
- Add the number of rectangular planes (3) and diagonal planes (6):
- Total planes of symmetry = 3 (rectangular) + 6 (diagonal) = 9.
6. Conclusion:
- Therefore, a cubic crystal possesses a total of 9 planes of symmetry.
Final Answer:
A cubic crystal possesses in all 9 planes of symmetry.
---
- A plane of symmetry is an imaginary plane that divides a crystal into two equal halves, where one half is the mirror image of the other.
- Visualize the cubic crystal structure. A cube has three axes: the x-axis, y-axis, and z-axis.
- A cube has three rectangular planes of symmetry, which are aligned with the axes:
- One plane parallel to the yz-plane (dividing the cube into left and right halves).
- One plane parallel to the xz-plane (dividing the cube into front and back halves).
- One plane parallel to the xy-plane (dividing the cube into top and bottom halves).
- A cube also has six diagonal planes of symmetry. These planes cut through the cube diagonally:
- Each diagonal plane connects opposite edges of the cube.
- There are two diagonal planes for each pair of opposite faces (front-back, left-right, top-bottom).
- Add the number of rectangular planes (3) and diagonal planes (6):
- Total planes of symmetry = 3 (rectangular) + 6 (diagonal) = 9.
- Therefore, a cubic crystal possesses a total of 9 planes of symmetry.
A cubic crystal possesses in all 9 planes of symmetry.
Topper's Solved these Questions
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - IMPECCABLE
49 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - ILLUSTRATIONS
24 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - ENABLE
50 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
- THEORY OF SOLUTIONSBOOK - VMC MODULES ENGLISHCHAPTER - THEORY OF SOLUTIONSEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
Knowledge Check
All protozoans possess
Aholozoic nutritionBcontractile vacuoleCpseudopodiaDeukaryotic organisationWhich of the following having plane of symmetry?
A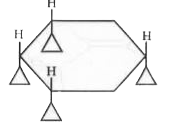 B
B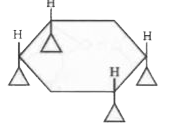 C
C DAll of these
DAll of these
Which species exhibits a plane of symmetry ?
View SolutionAll chordates possess
View SolutionAn angle having equal arms possesses how many lines of symmetry ? Show all possible lines of symmetry in such an angle.
View SolutionWhich of the following has plane of symmetry:-
View SolutionWhich of the follwing objects listed below possess a plane of symmetry and are, therfore, achiral?
a. A hammer
b. A car
c. A woodscrew
d. An ear
e. A screwdriver
f. A tennis shoe
g. A golf club
h. A baseball bat
View SolutionWhich of the following molecules possess a plane of symmetry ?
View Solution
